
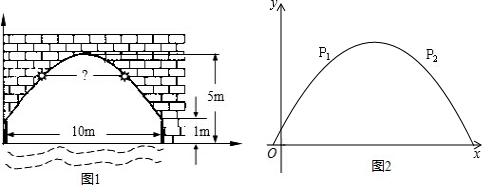
分析 (1)由图形可知这是一条抛物线,根据图形也可以知道抛物线的顶点坐标为(5,5),与y轴交点坐标是(0,1),设出抛物线的解析式将两点代入可得抛物线方程;
(2)第二题中要求灯的距离,只需要把纵坐标为4代入,求出x,然后两者相减,就是它们的距离.
解答 解:(1)抛物线的顶点坐标为(5,5),与y轴交点坐标是(0,1),
设抛物线的解析式是y=a(x-5)2+5,
把(0,1)代入y=a(x-5)2+5,
得a=-$\frac{4}{25}$,
∴y=-$\frac{4}{25}$(x-5)2+5(0≤x≤10);
(2)由已知得两景观灯的纵坐标都是4,
∴4=-$\frac{4}{25}$(x-5)2+5,
∴$\frac{4}{25}$(x-5)2=1,
∴x1=$\frac{15}{2}$,x2=$\frac{5}{2}$,
∴两景观灯间的距离为 $\frac{15}{2}$-$\frac{5}{2}$=5米.
点评 本题主要考查了二次函数的应用以及一元二次方程与二次函数的关系,从图象中可以看出的坐标是解题的关键.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:解答题
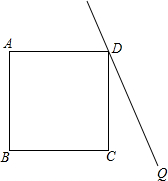 如图,在正方形ABCD外侧作直线DQ,点C关于直线DQ的对称点为P,连接DP、AP,AP交直线DQ于点F,交BD于点E.
如图,在正方形ABCD外侧作直线DQ,点C关于直线DQ的对称点为P,连接DP、AP,AP交直线DQ于点F,交BD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 25.30千克 | B. | 24.70千克 | C. | 25.51千克 | D. | 24.82千克 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 12 | C. | 13 | D. | 25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com