
【题目】如图,Rt△ABC中,∠CAB=90°,在斜边CB上取点M,N(不包含C、B两点),且tanB=tanC=tan∠MAN=1,设MN=x,BM=n,CN=m,则以下结论能成立的是( )

A. m=n B. x=m+n C. x>m+n D. x2=m2+n2
【答案】D
【解析】
将△ABM绕点A顺时针旋转90°至△ACN′,连接NN′;证明△AMN≌△ANN′,则有MN=NN′;在Rt△NN'C′中,根据勾股定理可得结论.
∵tanB=tanC=tan∠MAN=1,
∴∠B=∠C=∠MAN=45°,
∵∠CAB=90°,
∴AC=AB,
将△BAM绕点A顺时针旋转90°至△ACN′,点B与点C重合,点M落在N′处,连接NN′,
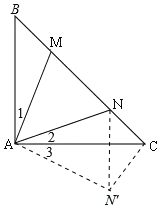
则有AN′=AM,CN′=BM,∠1=∠3,
∵∠MCN=45°,
∴∠1+∠2=45°,
∴∠2+∠3=45°,
∴∠NAN′=∠MAN.
在△MAN与△NAN′中,
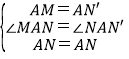 ,
,
∴△MAN≌△NCN′(SAS),
∴MN=NN′,
由旋转性质可知,∠ACN′=∠B=45°,
∴∠NCN′=∠ACN′+∠ACB=90°,
∴NN'2=NC2+N'C2,
即x2=n2+m2,
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,与AB交于点N,连接OM,ON,MN.下列四个结论:①△CNB≌△DMC;②OM=ON;③△OMN∽△OAD;④AN2+CM2=MN2,其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①a+b+c>0;②a﹣b+c>0;③abc<0;④2a+b=0.其中正确的个数为( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新能源汽车环保节能,越来越受到消费者的喜爱.各种品牌相继投放市场.一汽贸公司经销某品牌新能源汽车.去年销售总额为5000万元,今年1~5月份,每辆车的销售价格比去年降低1万元.销售数量与去年一整年的相同.销售总额比去年一整年的少20%,今年1~5月份每辆车的销售价格是多少万元?设今年1~5月份每辆车的销售价格为x万元.根据题意,列方程正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
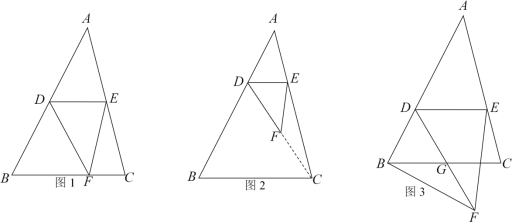
【题目】已知△ABC中,∠B= 60°,点D是AB边上的动点,过点D作DE∥BC交AC于点E,将△ABE沿DE折叠,点A对应点为F点.
(1)如图1,当点F恰好落在BC边上,求证:△BDF是等边三角形;
(2)如图2,当点F恰好落在△ABC内,且DF的延长线恰好经过点C,CF=EF,求∠A的大小;
(3)如图3,当点F恰好落在△ABC外,DF交BC于点G,连接BF,若BF⊥AB,AB=9,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将 ![]() 进行折叠,使得点
进行折叠,使得点 ![]() 与点
与点 ![]() 重合,折痕分别与边
重合,折痕分别与边 ![]() ,
,![]() 交于点
交于点 ![]() ,
,![]() ,点
,点 ![]() 关于直线
关于直线 ![]() 的对称点为点
的对称点为点 ![]() .
.
(1)画出直线 ![]() 和点
和点 ![]() ;
;
(2)连接 ![]() ,
,![]() ,若
,若 ![]() ,
,![]() ,则
,则 ![]() ;
;
(3)若 ![]() ,
,![]() ,则
,则 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com