练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知二次函数y=ax2+bx+c的图象如图所示，下列结论：①a+b+c＞0；②a﹣b+c＞0；③abc＜0；④2a+b=0．其中正确的个数为（ ）

    A.1个 B.2个 C.3个 D.4个

    【答案】A

    【解析】

    试题由抛物线的开口方向判断a的符号，由抛物线与y轴的交点判断c的符号，然后根据对称轴及抛物线中自变量x=1及x=﹣1的情况进行推理，进而对所得结论进行判断．

    解：①当x=1时，y=a+b+c＜0，错误；

    ②当x=﹣1时，y=a﹣b+c＞0，正确；

    ③由抛物线的开口向下知a＜0，与y轴的交点为在y轴原点，c=0，对称轴为x=＜0，a、b同号，即b＜0，因此abc=0，错误；

    ④∵对称轴为x==﹣1，得2a﹣b=0，错误；

    故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

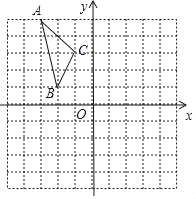
    【题目】如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣2，1），C（﹣1，3）．

    （1）画出△ABC和△A1B1C1关于原点O对称，画出△A1B1C1，并写出△A1B1C1的各顶点的坐标；

    （2）将△ABC绕着点O按顺时针方向旋转90°得到的△A2B2C2，画出△A2B2C2，并写出△A2B2C2的各顶点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点F是ABCD的边AD上的三等分点，BF交AC于点E，如果△AEF的面积为2，那么四边形CDFE的面积等于( )

    A. 18 B. 22 C. 24 D. 46

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1），P为△ABC所在平面上一点，且∠APB=∠BPC=∠CPA=120°，则点P叫做△ABC的费马点．

    （1）如果点P为锐角△ABC的费马点，且∠ABC=60°．

    ①求证：△ABP∽△BCP；

    ②若PA=3，PC=4，则PB= ．

    （2）已知锐角△ABC，分别以AB、AC为边向外作正△ABE和正△ACD，CE和BD 相交于P点．如图（2）

    ①求∠CPD的度数；

    ②求证：P点为△ABC的费马点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知,在△ABC中,BC=3,∠A=22.5°,将△ABC翻折使得点B与点A重合,折痕与边AC交于点P,如果AP=4,那么AC的长为_______

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】根据要求解方程

    （1）x2+3x﹣4=0（公式法）；

    （2）x2+4x﹣12=0（配方法）；

    （3）（x+3）（x﹣1）=5；

    （4）（x+4）2=5（x+4）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

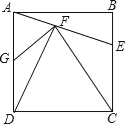
    【题目】如图，正方形ABCD中，E为BC中点连接AE，DF⊥AE于点F，连接CF，FG⊥CF交AD于点G，下列结论：①CF=CD；②G为AD中点；③△DCF∽△AGF；④，其中结论正确的个数有（　　）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABC中，∠CAB=90°，在斜边CB上取点M，N（不包含C、B两点），且tanB=tanC=tan∠MAN=1，设MN=x，BM=n，CN=m，则以下结论能成立的是（　　）

    A. m=n B. x=m+n C. x＞m+n D. x2=m2+n2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知点A、D、C、F在同一条直线上，AB=DE，BC=EF，要使△ABC≌△DEF，还需要添加一个条件是（　　）

    A. ∠BCA=∠F； B. ∠B=∠E； C. BC∥EF ； D. ∠A=∠EDF

    查看答案和解析>>

    同步练习册答案