
【题目】如图,在四边形ABCD中,AB=![]() ,AD=7,BC=8,tan∠B=
,AD=7,BC=8,tan∠B=![]() ,∠C=∠D,则线段CD的长为_____.
,∠C=∠D,则线段CD的长为_____.

【答案】![]()
【解析】
作AH⊥BC于H,在CB上截取CE,使得CE=AD,连接AE,作DM⊥AE于M,CN⊥AE于N.构造等腰梯形,把等腰梯形分成两个全等三角形一个矩形解决问题即可.
如图,作AH⊥BC于H,在CB上截取CE,使得CE=AD,连接AE,作DM⊥AE于M,CN⊥AE于N,
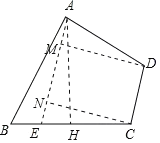
∵∠ADC=∠ECD,DA=CE,
∴四边形ADCE是等腰梯形,则△ADM≌△ECN,可得AM=EN,四边形MNCD是矩形,可得CD=MN,
在Rt△ABH中,∵tanB=![]() ,AB=
,AB=![]() ,
,
∴AH=5,BH=2,
∵BC=8,EC=AD=7,
∴BE=87=1,
∴EH=BHBE=1,
在Rt△AEH中,AE=![]() =
=![]() ,
,
∵△ECN∽△EAH,
∴![]() ,
,
∴EN=![]() ,
,
∴AM=EN=![]() ,
,
∴CD=MN=AEAMEN=![]() ,
,
故答案为:![]() .
.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
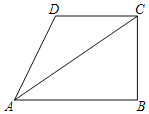
【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,连接AC,∠DAC=∠BAC.
(1)求证:AD=DC;
(2)若∠D=120°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据要求解方程
(1)x2+3x﹣4=0(公式法);
(2)x2+4x﹣12=0(配方法);
(3)(x+3)(x﹣1)=5;
(4)(x+4)2=5(x+4).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BF和CE分别是钝角△ABC(∠ABC是钝角)中AC、AB边上的中线,又BF⊥CE,垂足是G,过点G作GH⊥BC,垂足为H.
(1)求证:GH2=BHCH;
(2)若BC=20,并且点G到BC的距离是6,则AB的长为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠CAB=90°,在斜边CB上取点M,N(不包含C、B两点),且tanB=tanC=tan∠MAN=1,设MN=x,BM=n,CN=m,则以下结论能成立的是( )

A. m=n B. x=m+n C. x>m+n D. x2=m2+n2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或化简:
(1)sin45°cos60°﹣cos45°sin30°;
(2)5tan30°﹣2(cos60°﹣sin60°);
(3)(![]() tan30°)2005(2
tan30°)2005(2![]() sin45°)2004;
sin45°)2004;
(4)![]() (2cos45°﹣tan45°)﹣(tan60°+sin30°)0﹣(2sin45°﹣1)﹣1.
(2cos45°﹣tan45°)﹣(tan60°+sin30°)0﹣(2sin45°﹣1)﹣1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上(如图),求此时货轮距灯塔A的距离AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
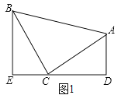
【题目】(1)(模型建立)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED与D,过B作BE⊥ED于E,求证:△BEC≌△CDA;
(2)(模型应用):已知直线![]() 与y轴交于A点,与x轴交于B点,将线段AB绕点B逆时针旋转90度,得到线段BC,过点A,C作直线,求直线AC的解析式;
与y轴交于A点,与x轴交于B点,将线段AB绕点B逆时针旋转90度,得到线段BC,过点A,C作直线,求直线AC的解析式;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(﹣1,2).
(k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(﹣1,2).

(1)求反比例函数的解析式;
(2)连接EF,求△BEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com