
【题目】用棋子摆成的“![]() ”字形图,如图所示:
”字形图,如图所示:
 ……
……
(1)填写下表:
图案序号 | ① | ② | ③ | ④ | … | ⑩ |
每个图案中棋子的个数 |
|
| ______ | _____ | … | ______ |
(2)写出第![]() 个“
个“![]() ”字形图案中棋子的个数(用含
”字形图案中棋子的个数(用含![]() 的代数式表示):
的代数式表示):
(3)第20个“![]() ”字形图案共有棋子多少个?
”字形图案共有棋子多少个?
【答案】(1)11,14,32;(2)摆成第n个图案需![]() 枚棋子(3)62枚棋子
枚棋子(3)62枚棋子
【解析】
(1)通过观察已知图形可得:每个图形都是在5的基础上依次多3枚,得出摆成第③④⑩个图形需要的棋子数;
(2)由(1)得出的规律为摆成第n个图案需![]() 枚棋子;
枚棋子;
(3)将n=20代入(2)中规律计算即可求解.
(1)首先观察图形,得到前面三个图形的具体个数,不难发现:在5的基础上依次多3枚.即第n个图案需要![]() .
.
那么当n=3时,则有11枚;当n=4时,则有14枚;当n=10时,则有32枚;
故答案为:11,14,32
(2)因为第①个图案有5枚棋子,
第②个图案有(5+3×1)枚棋子,
第③个图案有(5+3×2)枚棋子,
依此规律可得第n个图案需![]() 枚棋子.
枚棋子.
(3)第20个“![]() ”字形图案共有棋子
”字形图案共有棋子![]() (枚)
(枚)
即第20个“![]() ”字形图案共有62枚棋子.
”字形图案共有62枚棋子.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为迎军运会,武汉市对城区主干道进行绿化,计划把某一段公路的两侧全部栽上银杏树,要求每两棵树的间隔相等,并且路的每一侧的两端都各栽一棵,如果每隔4米栽一棵,则还差102棵;如果每隔5米栽一棵,则多出102棵,设公路长x米,有y棵树,则下列方程中:①2(![]() +1)﹣102=2(
+1)﹣102=2(![]() +1)+102;②
+1)+102;②![]() ﹣102=
﹣102=![]() +102;③4(
+102;③4(![]() ﹣1)=5(
﹣1)=5(![]() ﹣1);④4(
﹣1);④4(![]() ﹣1)=5(
﹣1)=5(![]() ﹣1),其中正确的是( )
﹣1),其中正确的是( )
A.①③B.②③C.①④D.①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A.B在数轴上对应的有理数分别是a,b那么A.B之间的距离可以表示为AB=a-b,点P是数轴上一动点,对应数为x,则点P与点A,B的距离分别表示为PA=x-a,PB=x-b,且a+4+![]() =0.
=0.
(1)直接写出a,b的值;
(2)当![]() =2时,求x的值;
=2时,求x的值;
(3)当点P在数轴上运动时,是否存在这样的x,使![]() ?若存在,请求出的x的值;若不存在,请说明理由。
?若存在,请求出的x的值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)(﹣2.4)+(﹣3.7)+(﹣4.6)+5.7
(2)﹣20+(﹣14)﹣(﹣18)﹣13
(3)![]()
(4)(﹣3![]() )+12.5+(16
)+12.5+(16![]() )﹣(﹣2.5)
)﹣(﹣2.5)
(5)0.75+0.125+(﹣2![]() )﹣(﹣12
)﹣(﹣12![]() )+(﹣4
)+(﹣4![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
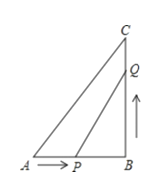
【题目】如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,动点P从点A开始沿AB边向B以1cm/s的速度移动(不与点B重合);动点Q从B点开始沿BC边向点C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,出发多少秒后,四边形APQC的面积为16cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图.拼完后,小华看来看去总觉得所拼图形似乎存在问题.
![]()
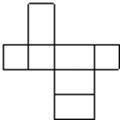
(1)请你帮小华分析一下拼图是否存在问题:若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全.
(2)若图中的正方形边长为2cm,长方形的长为3cm,宽为2cm,请直接写出修正后所折叠而成的长方体的容积: _________ cm3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”,图中点A表示﹣12,点B表示12,点C表示20,我们称点A和点C在数轴上相距32个长度单位,动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速,设运动的时间为t秒,问:
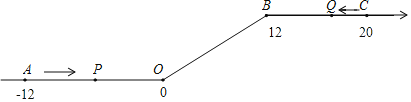
(1)动点Q从点C运动至点A需要 秒;
(2)P、Q两点相遇时,求出t的值及相遇点M所对应的数是多少?
(3)求当t为何值时,A、P两点在数轴上相距的长度是C、Q两点在数轴上相距的长度的![]() 倍(即P点运动的路程=
倍(即P点运动的路程=![]() Q点运动的路程).
Q点运动的路程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com