
【题目】图(1)是一个蒙古包的照片,这个蒙古包可以近似看成是圆锥和圆柱组成的几何体,如图(2)所示.
(1)请画出这个几何体的俯视图;
(2)图(3)是这个几何体的正面示意图,已知蒙古包的顶部离地面的高度EO1=6米,圆柱部分的高OO1=4米,底面圆的直径BC=8米,求∠EAO的度数(结果精确到0.1°).
【答案】
(1)
画出俯视图,如图所示

(2)
解:连接EO1,如图所示:
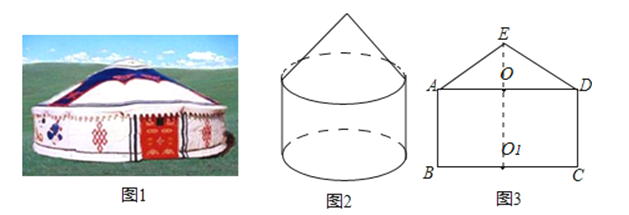
∵EO1=6米,OO1=4米,
∴EO=EO1﹣OO1=6﹣4=2米,
∵AD=BC=8米,
∴OA=OD=4米,
在Rt△AOE中,tan∠EAO=![]() =
=![]() =
=![]() ,
,
则∠EAO≈26.6°.
【解析】(1)根据图2,画出俯视图即可;
(2)连接EO1 , 如图所示,由EO1﹣OO1求出EO的长,由BC=AD,O为AD中点,求出OA的长,在直角三角形AOE中,利用锐角三角函数定义求出tan∠EAO的值,即可确定出∠EAO的度数.
【考点精析】掌握圆锥的相关计算和圆柱的相关计算是解答本题的根本,需要知道圆锥侧面展开图是一个扇形,这个扇形的半径称为圆锥的母线;圆锥侧面积S=πrl;V圆锥=1/3πR2h.;圆柱的体积: V圆柱=πR2h.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】有六张完全相同的卡片,其正面分别标有数字:﹣2,![]() ,π,0,
,π,0,![]() ,
,![]() ,将它们背面朝上洗匀后,从中随机抽取一张卡片,则其正面的数字为无理数的概率是 .
,将它们背面朝上洗匀后,从中随机抽取一张卡片,则其正面的数字为无理数的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.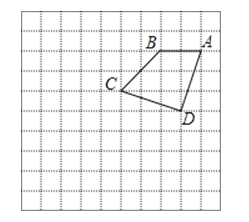
(1)在图中画出四边形AB′C′D′;
(2)填空:△AC′D′是 三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD内接于⊙O,∠ADC=90°,∠DCB<90°,对角线AC平分∠DCB,延长DA,CB相交于点E.
(1)如图1,EB=AD,求证:△ABE是等腰直角三角形;
(2)如图2,连接OE,过点E作直线EF,使得∠OEF=30°,当∠ACE≥30°时,判断直线EF与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,顶点为A(1,﹣1)的抛物线经过点B(5,3),且与x轴交于C,D两点(点C在点D的左侧).
(1)求抛物线的解析式;
(2)求点O到直线AB的距离;
(3)点M在第二象限内的抛物线上,点N在x轴上,且∠MND=∠OAB,当△DMN与△OAB相似时,请你直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A是∠MON边OM上一点,AE∥ON. 
(1)在图中作∠MON的角平分线OB,交AE于点B;(要求:尺规作图,保留作图痕迹,不写作法和证明)
(2)在(1)中,过点A画OB的垂线,垂足为点D,交ON于点C,连接CB,将图形补充完整,并证明四边形OABC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2bx+c
(1)若抛物线的顶点坐标为(2,﹣3),求b,c的值;
(2)若b+c=0,是否存在实数x,使得相应的y的值为1,请说明理由;
(3)若c=b+2且抛物线在﹣2≤x≤2上的最小值是﹣3,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( )

A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组同学在一周内阅读课外科普读物与人数情况如表所示:
课外科普读物(本数) | 4 | 5 | 6 |
人数 | 3 | 2 | 1 |
下列关于“课外科普读物”这组数据叙述正确的是
A.中位数是3
B.众数是4
C.平均数是5
D.方差是6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com