
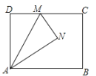
【题目】如图,矩形ABCD中,AB=5,AD=4,M是边CD上一点,将△ADM沿直线AM对折,得△ANM,连BN,若DM=1,则△ABN的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
延长MN交AB延长线于点Q,由矩形的性质得出∠DMA=∠MAQ,由折叠性质得出∠DMA=∠AMQ,AN=AD=4,MN=MD=1,得出∠MAQ=∠AMQ,证出MQ=AQ,设NQ=x,则AQ=MQ=1+x,证出∠ANQ=90°,在Rt△ANQ中,由勾股定理得出方程,解方程求出NQ=7.5,AQ=8.5,即可求出△ABN的面积.
解:延长MN交AB延长线于点Q,
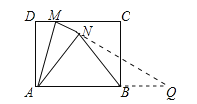
∵四边形ABCD是矩形,
∴AB∥DC,
∴∠DMA=∠MAQ,
由折叠性质得:△ANM≌△ADM,
∴∠DMA=∠AMQ,AN=AD=4,MN=MD=1,
∴∠MAQ=∠AMQ,
∴MQ=AQ,
设NQ=x,则AQ=MQ=1+x,
∵∠ANM=90°,
∴∠ANQ=90°,
在Rt△ANQ中,由勾股定理得:AQ2=AN2+NQ2,
∴(x+1)2=42+x2,
解得:x=7.5,
∴NQ=7.5,AQ=8.5,
∵AB=5,AQ=8.5,
∴S△NAB=![]() S△NAQ=
S△NAQ=![]() ×
×![]() ANNQ=
ANNQ=![]() ×
×![]() ×4×7.5=
×4×7.5=![]() ;
;
故选:D.


科目:初中数学 来源: 题型:
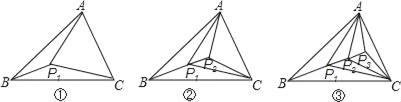
【题目】如图,△ABC的三个顶点和它内部的点P1,把△ABC分成3个互不重叠的小三角形;△ABC的三个顶点和它内部的点P1、P2,把△ABC分成5个互不重叠的小三角形;△ABC的三个顶点和它内部的点 P1、P2、P3,把△ABC分成7个互不重叠的小三角形;…△ABC的三个顶点和它内部的点 P1、P2、P3、…、P2017,把△ABC分成_____个互不重叠的小三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推动阳光体育活动的广泛开展,引导学生积极参加体育锻炼,学校准备购买一批运动鞋供学生借用.现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据图中提供的信息,解答下列问题:

(1)本次接受随机抽样调查的学生人数为 人,图①中的m的值为 ,图①中“38号”所在的扇形的圆心角度数为 ;
(2)本次调查获取的样本数据的众数是 ,中位数是 ;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买36号运动鞋多少双?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区对即将参加中考的4 000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图.请根据图表信息回答下列问题:
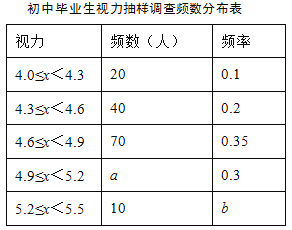
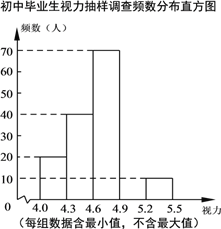
(1)本次调查样本容量为 ;
(2)在频数分布表中,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在4.9以上(含4.9)均属标准视力,根据上述信息估计全区初中毕业生中达到标准视力的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,2),B(﹣2,6),C(0,4)是直角坐标系中的三点.
(1)把△ABC绕着点O顺时针方向旋转90°,得到△A1B1C1,画出旋转后的图形,并写出点A的对应点A1的坐标;
(2)以原点O为位似中心,将△ABC缩小为原来的一半,请在所给的坐标系中作出所有满足条件的图形.
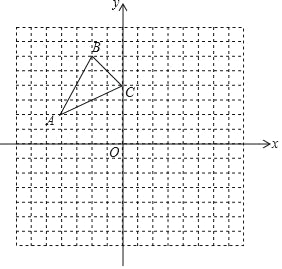
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料130kg,乙种原料144kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5kg,乙种原料4kg,且每件A产品可获利700元;生产每件B产品需甲种原料3kg,乙种原料6kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种;
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解福清七年级学生的视力情况,现从全市七年级学生中随机抽取![]() 名学生进行调查,下列说法不正确的是一项是( )
名学生进行调查,下列说法不正确的是一项是( )
A.这种调查是抽样调查B.个体是每个学生的视力情况
C.样本容量是![]() D.若抽到的都是城区学生,则样本更具有代表性
D.若抽到的都是城区学生,则样本更具有代表性
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )
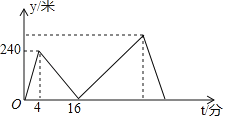
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点A,B分别对应数a,b,其中a<0,b>0.
(1)当a=﹣2,b=6时,线段AB的中点对应的数是 ;(直接填结果)
(2)若该数轴上另有一点M对应着数m.
①当m=2,b>2,且AM=2BM时,求代数式a+2b+20的值;
②当a=﹣2,且AM=3BM时,请说明代数式3b﹣4m或2m﹣3b均有定值(不变的数值),并求出它们的定值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com