
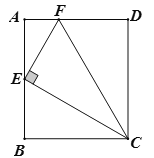
【题目】如图,在矩形![]() 中,点
中,点![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,下列结论:
,下列结论:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④若![]() ,则
,则![]() .
.
其中正确的结论是______________.(填写所有正确结论的序号)
【答案】①③④
【解析】
根据矩形的性质和余角的性质可判断①;延长CB,FE交于点G,根据ASA可证明△AEF≌△BEG,可得AF=BG,EF=EG,进一步即可求得AF、BC与CF的关系,S△CEF与S△EAF+S△CBE的关系,进而可判断②与③;由![]() ,结合已知和锐角三角函数的知识可得
,结合已知和锐角三角函数的知识可得![]() ,进一步即可根据AAS证明结论④;问题即得解决.
,进一步即可根据AAS证明结论④;问题即得解决.
解:∵![]() ,
,![]() ,
,
∵四边形ABCD是矩形,∴∠B=90°,∴![]() ,
,
![]() ,所以①正确;
,所以①正确;
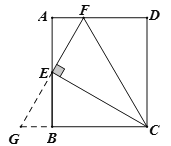
延长CB,FE交于点G,如图,
在△AEF和△BEG中,∵∠FAE=∠GBE=90°,AE=BE,∠AEF=∠BEG,
∴△AEF≌△BEG(ASA),∴AF=BG,EF=EG,∴S△CEG=S△CEF,
∵CE⊥EG,∴CG=CF,∴AF+BC=BG+BC=CG=CF,所以②错误;
∴S△CEF=S△CEG=S△BEG+S△CBE=S△EAF+S△CBE,所以③正确;
若![]() ,则
,则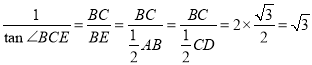 ,
,![]() ,
,![]() ,
,
在![]() 和
和![]() 中,∵∠CEF=∠D=90°,
中,∵∠CEF=∠D=90°,![]() ,CF=CF,
,CF=CF,![]() ≌
≌![]() ,所以④正确.
,所以④正确.
综上所述,正确的结论是①③④.
故答案为:①③④.


科目:初中数学 来源: 题型:
【题目】“校园安全”越来越受到人们的关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:

(1)接受问卷调查的学生共有______人,条形统计图中m的值为______;
(2)扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为______;
(3)若该中学共有学生1800人,根据上述调查结果,可以估计出该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为______人;
(4)若从对校园安全知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加校园安全知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() 是对角线
是对角线![]() 上一个动点(不与点
上一个动点(不与点![]() 重合),连接
重合),连接![]() 过点
过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() .作
.作![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
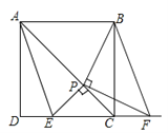
(1)由题意易知,![]() ,观察图,请猜想另外两组全等的三角形
,观察图,请猜想另外两组全等的三角形![]()
![]() ;
;![]()
![]() ;
;
(2)求证:四边形![]() 是平行四边形;
是平行四边形;
(3)已知![]() ,
,![]() 的面积是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
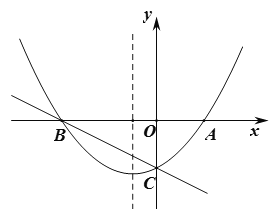
【题目】如图,对称轴是![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,
![]() 求抛物线的函数表达式;
求抛物线的函数表达式;
![]() 若点
若点![]() 是直线
是直线![]() 下方的抛物线上的动点,求
下方的抛物线上的动点,求![]() 的面积的最大值;
的面积的最大值;
![]() 若点
若点![]() 在抛物线对称轴左侧的抛物线上运动,过点
在抛物线对称轴左侧的抛物线上运动,过点![]() 作
作![]() 铀于点
铀于点![]() ,交直线
,交直线![]() 于点
于点![]() ,且
,且![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 在对称轴上是否存在一点
在对称轴上是否存在一点![]() ,使
,使![]() 的周长最小,若存在,请求出
的周长最小,若存在,请求出![]() 点的坐标和
点的坐标和![]() 周长的最小值;若不存在,请说明理由.
周长的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2-2m2x+2交y轴于点A,交直线x=4于点B.
(1)抛物线的对称轴为x=____________(用含m的代数式表示)
(2)若AB∥x轴,求抛物线的解析式.
(3)记抛物线在A、B之间的部分为图象G(包含A、B两点),若对于图象G上任意一点P(xp,yp),都有yp≤2,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解七年级400名学生读书情况,随机调查了七年级50名学生读书的册数.统计数据如下表所示:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 3 | 13 | 16 | 17 | 1 |
(1)求这50个样本数据的平均救,众数和中位数;
(2)根据样本数据,估计该校七年级400名学生在本次活动中读书多于3册的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
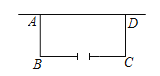
【题目】某校在基地参加社会活动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留有一个宽为3米的出入口,如图所示.如何设计才能使园地的面积![]() 最大?下面是两位同学争议的情境:小军:把它围成一个正方形,这样的面积一定最大.小英:不对啦!面积最大的不是正方形.请根据上面信息,解决问题:
最大?下面是两位同学争议的情境:小军:把它围成一个正方形,这样的面积一定最大.小英:不对啦!面积最大的不是正方形.请根据上面信息,解决问题:
(1)设![]() 米(
米(![]() ).
).
①![]() 米(用含
米(用含![]() 的代数式表示);
的代数式表示);
②![]() 的取值范围是 ;
的取值范围是 ;
(2)请你判断谁的说法正确,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com