
【题目】这是一道我们曾经探究过的问题:如图1.等腰直角三角形![]() 中,
中,![]() ,
,![]() .直线
.直线![]() 经过点
经过点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() .易证得
.易证得![]() ≌
≌![]() .(无需证明),我们将这个模型称为“一线三等角”或者叫“K形图”.接下来,我们就利用这个模型来解决一些问题:
.(无需证明),我们将这个模型称为“一线三等角”或者叫“K形图”.接下来,我们就利用这个模型来解决一些问题:
(模型应用)
(1)如图2.已知直线l1:![]() 与与坐标轴交于点A、B.以AB为直角边作等腰直角三角形ABC,若存在,请求出C的坐标;不存在,若说明理由.
与与坐标轴交于点A、B.以AB为直角边作等腰直角三角形ABC,若存在,请求出C的坐标;不存在,若说明理由.

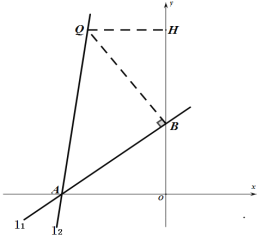
(2)如图3已知直线l1:![]() 与坐标轴交于点A、B.将直线l1绕点A逆时针旋转45°至直线l2.直线l2在x轴上方的图像上是否存在一点Q,使得△QAB是以QA为底的等腰直角三角形?若存在,请求出直线BQ的函数关系式;若不存在,说明理由.
与坐标轴交于点A、B.将直线l1绕点A逆时针旋转45°至直线l2.直线l2在x轴上方的图像上是否存在一点Q,使得△QAB是以QA为底的等腰直角三角形?若存在,请求出直线BQ的函数关系式;若不存在,说明理由.
(拓展延伸)
(3)直线AB:![]() 与
与![]() 轴负半轴、
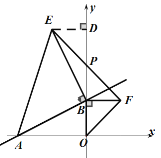
轴负半轴、![]() 轴正半轴分别交于A、B两点.分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交y轴于P点,如图4,△EPB的面积是否确定?若确定,请求出具体的值;若不确定,请说明理由.
轴正半轴分别交于A、B两点.分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交y轴于P点,如图4,△EPB的面积是否确定?若确定,请求出具体的值;若不确定,请说明理由.
【答案】(1)存在,![]() 或
或![]() 或
或![]() 或
或![]() ;(2)存在,
;(2)存在,![]() ;(3)确定,面积是:1.
;(3)确定,面积是:1.
【解析】
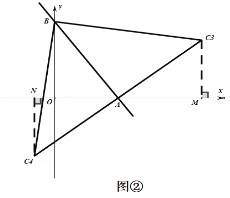
(1)存在,如图①、图②,C1、C2、C3、C4都符合,根据“一线三等角”模型,易证得三角形全等,从而求得点C的坐标;
(2)存在,过![]() 作
作![]() 交直线l2于
交直线l2于![]() ,△QAB就是以QA为底边的等腰直角三角形,根据“一线三等角”模型,易证得
,△QAB就是以QA为底边的等腰直角三角形,根据“一线三等角”模型,易证得![]() , 从而求得点Q的坐标,继而求得直线BQ的函数关系式;
, 从而求得点Q的坐标,继而求得直线BQ的函数关系式;
(3)确定,面积是:1.过![]() 作
作![]() 轴于
轴于![]() ,根据“一线三等角”模型,易证得
,根据“一线三等角”模型,易证得![]() ,可求得E、F的坐标,从而求得直线EF的解析式,继而求得P点坐标,可以求得△EPB的面积.
,可求得E、F的坐标,从而求得直线EF的解析式,继而求得P点坐标,可以求得△EPB的面积.
(1)∵直线l1:![]() 与与坐标轴交于点A、B,
与与坐标轴交于点A、B,
∴A、B的坐标分别是A(3,0)、B(0,4),则![]() ,
,
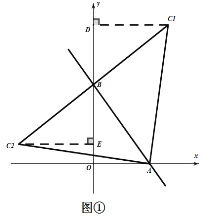
如图①:过![]() 作
作![]() 轴于
轴于![]() ,
,![]() 作
作![]() 轴于
轴于![]() ,
,
根据“一线三等角”模型,易证得![]()
∴![]()
∴![]() 的坐标是
的坐标是![]()
如图②:过![]() 作
作![]() 轴于
轴于![]() ,
,![]() 作
作![]() 轴于
轴于![]() ,
,
根据“一线三等角”模型,易证得![]() ,
,![]()
∴![]()
∴![]() 的坐标是
的坐标是![]()
(2)存在,
如图,过![]() 作
作![]() 交直线l2于
交直线l2于![]() ,
,
由于![]() 是旋转角,
是旋转角,
∴![]() ,
,
则△QAB就是以QA为底边的等腰直角三角形,
∵直线l1:![]() 与与坐标轴交于点A、B,
与与坐标轴交于点A、B,
∴A、B的坐标分别是A(-4,0)、B(0,3),
则![]() ,
,
过![]() 作
作![]() 轴于
轴于![]() ,
,
根据“一线三等角”模型,易证得![]()
∴![]()
∴![]() 的坐标是
的坐标是![]()
设直线BQ的解析式是:![]()
把B(0,3),![]() 代入得
代入得![]() ,
,
解得: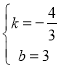
∴直线BQ的解析式是:![]()
(3)确定,面积是:1.
∵直线AB:![]() 与
与![]() 轴负半轴、
轴负半轴、![]() 轴正半轴分别交于A、B两点,
轴正半轴分别交于A、B两点,
∴A、B的坐标分别是A(-2,0)、B(0,1),
则![]() ,
,
如图,过![]() 作
作![]() 轴于
轴于![]() ,
,
根据“一线三等角”模型,易证得![]()
∴![]() ,
,
∴![]() 的坐标是
的坐标是![]()
∵![]() 是等腰直角三角形,∴
是等腰直角三角形,∴![]()
∴![]() 的坐标是
的坐标是![]()
设直线EF的解析式是:![]()
把![]() ,
,![]() 代入得
代入得![]() ,
,
解得:![]()
∴直线EF的解析式是:![]()
∴直线EF与轴的交点坐标是![]()
![]()


科目:初中数学 来源: 题型:
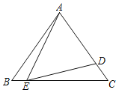
【题目】如图,在△ABC中,AB=AC=6,点D在边AC上,AD的中垂线交BC于点E.若∠AED=∠B,CE=3BE,则CD等于( )
A. ![]() B. 2C.
B. 2C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】许昌芙蓉湖位于许昌市水系建设总体规划中部,上游接纳清泥河来水,下游为鹿鸣湖等水系供水,承担着承上启下的重要作用,是利用有限的水资源、形成良好的水生态环境打造生态宜居城市的重要部分.某校课外兴趣小组想测量位于芙蓉湖两端的A,B两点之间的距离他沿着与直线AB平行的道路EF行走,走到点C处,测得∠ACF=45°,再向前走300米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为200米,求A,B两点之间的距离(结果保留一位小数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于
轴于![]() 、
、![]() 两点,且
两点,且![]() ,
,![]() 满足
满足![]() ,且
,且![]() ,
,![]() 是常数。直线
是常数。直线![]() 平分
平分![]() ,交
,交![]() 轴于
轴于![]() 点。
点。
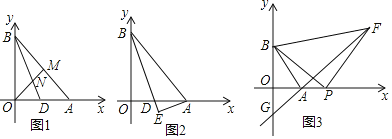
(1)若![]() 的中点为
的中点为![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() ;
;
(2)如图2,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,猜想
,猜想![]() 与
与![]() 间的数量关系,并证明你的猜想;
间的数量关系,并证明你的猜想;
(3)如图3,在![]() 轴上有一个动点
轴上有一个动点![]() (在
(在![]() 点的右侧),连接
点的右侧),连接![]() ,并作等腰
,并作等腰![]() ,其中
,其中![]() ,连接
,连接![]() 并延长交
并延长交![]() 轴于
轴于![]() 点,当
点,当![]() 点在运动时,
点在运动时,![]() 的长是否发生改变?若改变,请求出它的变化范围;若不变,求出它的长度.
的长是否发生改变?若改变,请求出它的变化范围;若不变,求出它的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在他家里的时钟上安装了一个电脑软件,他设定当钟声在n点钟响起后,下一次则在(3n﹣1)小时后响起,例如钟声第一次在3点钟响起,那么第2次在(3×3﹣1=8)小时后,也就是11点响起,第3次在(3×11﹣1=32)小时后,即7点响起,以此类推…;现在第1次钟声响起时为2点钟,那么第3次响起时为_____点,第2017次响起时为_____点(如图钟表,时间为12小时制).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠B=30°,O是BC上一点,以点O为圆心,OB长为半径作圆,恰好经过点A,并与BC交于点D.
(1)判断直线CA与⊙O的位置关系,并说明理由;
(2)若AB=4![]() ,求图中阴影部分的面积(结果保留π).
,求图中阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若经过一个三角形某一顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形过该顶点的生成三角形.

(1)如图,在等腰Rt△ABC中,AB=AC,∠A=90°,请问△ABC是否是生成三角形?请你说明理由.
(2)若△ABC是等腰三角形过顶点B的生成三角形,∠C是其最小的内角,请探求∠ABC与∠C之间的关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com