
已知二次函数的顶点坐标为A(1,﹣4),且经过点B(3,0).
(1)求该二次函数的解析式;
(2)判断点C(2,﹣3)、D(﹣1,1)是否在该函数图象上,并说明理由.
【考点】待定系数法求二次函数解析式;二次函数图象上点的坐标特征.
【分析】(1)设二次函数的解析式是y=a(x﹣h)2+k,先代入顶点A的坐标,再把B的坐标代入,即可求出a,即可得出解析式;
(2)把C、D的坐标分别代入,看看两边是否相等即可.
【解答】解:(1)设二次函数的解析式是y=a(x﹣h)2+k,
∵二次函数的顶点坐标为A(1,﹣4),
∴y=a(x﹣1)2﹣4,
∵经过点B(3,0),
∴代入得:0=a(3﹣1)2﹣4,
解得:a=1,
∴y=(x﹣1)2﹣4,
即二次函数的解析式为y=x2﹣2x﹣3;
(2)点C(2,﹣3)在该函数图象上,点D(﹣1,1)不在该函数图象上,
理由是:把C(2,﹣3)代入y=x2﹣2x﹣3得:左边=﹣3,右边=4﹣4﹣3=﹣3,
即左边=右边,
所以点C在该函数的图象上;
把D(﹣1,1)代入y=x2﹣2x﹣3得:左边=1,右边=1+2﹣3=0,
即左边≠右边,
所以点D不在该函数的图象上.
【点评】本题考查了用待定系数法求二次函数的解析式,二次函数图象上点的坐标特征的应用,能正确求出函数的解析式是解此题的关键.


科目:初中数学 来源: 题型:
如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.如果一条直线与果圆只有一个交点,则这条直线叫做果圆的切线.已知A、B、C、D四点为果圆与坐标轴的交点,E为半圆的圆心,抛物线的解析式为y=x2﹣2x﹣3,AC为半圆的直径.
(1)分别求出A、B、C、D四点的坐标;
(2)求经过点D的果圆的切线DF的解析式;
(3)若经过点B的果圆的切线与x轴交于点M,求△OBM的面积.


查看答案和解析>>
科目:初中数学 来源: 题型:
某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=﹣x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
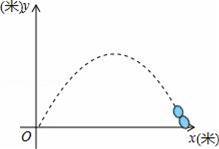

A.4米 B.3米 C.2米 D.1米
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,
(1)求抛物线所对应的函数解析式;
(2)求△ABD的面积;
(3)将△AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com