
分析 (1)根据二次函数y=-x2-mx-m+1与x轴有两个交点,利用根的判别式△>0,可以求出m的取值范围;
(2)令y=0,解-x2-mx-m+1=0可求得函数图象与x轴的两个交点坐标,根据题意确定A,B点的坐标,点A为(-1,0),点B为(1-m,0);再令x=0,求出点C为(0,1-m),以A.B.C三点为顶点的△ABC为等腰三角形共有三种情况:①CA=CB,②AB=AC,③BA=BC.①中根据题意可知A,B关于y轴对称,得到-1+(1-m)=0,解得m=0,从而求出解析式;②,③可以根据两点距离公式用含有m的代数式表示线段的长度,再根据相等的线段作为等量关系列出关于m的方程,解方程即可求解,然后再代入原方程看是否符合题意,取得符合题意的m的值,从而求出对应的函数解析式.
解答 解:(1)∵二次函数y=-x2-mx-m+1与x轴有两个交点
∴△=(-m)2-4×(-1)×(-m+1)=m2-4m+4=(m-2)2>0
∴m的取值范围为:m≠2的任何实数.
(2)令y=0,则-x2-mx-m+1=0
解得:x1=1-m,x2=-1
∴点A为(-1,0),点B为(1-m,0)
∵A点在B点的左边,两点中至少有一点在原点的右边
∴A点中原点左侧,B点中原点右侧
又∵函数图象与y轴交于点C,即点C中y轴上,且点C为(0,1-m)
当以A.B.C三点为顶点的△ABC为等腰三角形时分情况讨论:
①若CA=CB,即A,B关于y轴对称,那么-1+(1-m)=0,解得m=0;二次函数y=-x2+1
②若AB=AC,则AB2=AC2,
∵AC2=1+(1-m)2,AB2=(1-m+1)2
∴1+(1-m)2=(1-m+1)2,解得m=1,此时点B为(0,0),不合题意,故舍去;
③若BA=BC,则BA=$\sqrt{2}$(1-m),BC=2-m,则$\sqrt{2}$(1-m)=2-m,解得:m=-$\sqrt{2}$
二次函数y=-x2$+\sqrt{2}$x$+\sqrt{2}$+1.
点评 本题主要考查了抛物线与x轴交点与一元二次方程之间的关系.函数的图象与x轴的交点情况可以由△=b2-4ac来判断,同时也可以根据△值的范围来求出函数解析式中字母系数的取值范围.本题第2问中给出的条件△ABC为等腰三角形,并没有说明相等的线段,应该分三种情况进行讨论,再结合题目中的条件进行值的取舍.


科目:初中数学 来源: 题型:解答题
 如图,身高1.6m的小王晚上沿箭头方向散步至一路灯下,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部向东走20步到M处,发观自己的影子端点刚好在两盏路灯的中间点P处,继续沿刚才自己的影子走5步到P处,此时影子的端点在Q处.
如图,身高1.6m的小王晚上沿箭头方向散步至一路灯下,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部向东走20步到M处,发观自己的影子端点刚好在两盏路灯的中间点P处,继续沿刚才自己的影子走5步到P处,此时影子的端点在Q处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
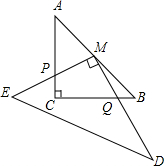 把一块直角三角板DEM的直角顶点M放在等腰的直角三角板ABC的斜边AB的中点M上,ME和MD分别交边AC、BC于点P、Q,求证:MP=MQ.
把一块直角三角板DEM的直角顶点M放在等腰的直角三角板ABC的斜边AB的中点M上,ME和MD分别交边AC、BC于点P、Q,求证:MP=MQ.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
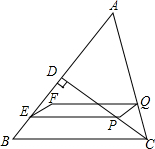 如图,在△ABC中,AC=BC=5cm,AB=6cm,CD⊥AB于点D.动点P、Q同时从点C出发,点P沿线CD做依次匀速往返运动,回到点C停止;点Q沿折线CA-AD向终点D做匀速运动;点P、Q运动的速度都是5cm/s.过点P作PE∥BC,交AB于点E,连结PQ.当点P、E不重合点P、Q不重合时,以线段PE∥BC,交AB于点E,连结PQ.当点P、E不重合且点P、Q不重合时,以线段PE、PQ为一组邻边作?PEFQ.设点P运动的时间为t(s),?PEFQ与△ABC重叠部分的面积为S(cm2).
如图,在△ABC中,AC=BC=5cm,AB=6cm,CD⊥AB于点D.动点P、Q同时从点C出发,点P沿线CD做依次匀速往返运动,回到点C停止;点Q沿折线CA-AD向终点D做匀速运动;点P、Q运动的速度都是5cm/s.过点P作PE∥BC,交AB于点E,连结PQ.当点P、E不重合点P、Q不重合时,以线段PE∥BC,交AB于点E,连结PQ.当点P、E不重合且点P、Q不重合时,以线段PE、PQ为一组邻边作?PEFQ.设点P运动的时间为t(s),?PEFQ与△ABC重叠部分的面积为S(cm2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com