
【题目】已知二次函数y=x2﹣2x﹣3
(1)求函数图象的顶点坐标,与坐标轴的交点坐标,并画出函数的大致图象;
(2)根据图象直接回答:当y<0时,求x的取值范围;当y>﹣3时,求x的取值范围.
【答案】(1)顶点坐标为(1,4),与x轴的交点坐标为(﹣1,0),(3,0),与y轴的交点坐标为(0,﹣3),作图见解析;(2)当﹣1<x<3时,y<0;当x<0或x>1时,y>﹣3.
【解析】
(1)利用配方法得到y=(x﹣1)2﹣4,从而得到抛物线的顶点坐标,再计算自变量为0对应的函数值得到抛物线与y轴的交点坐标,通过解方程x2﹣2x﹣3=0得抛物线与x轴的交点坐标,然后利用描点法画函数图象;
(2)结合函数图象,当y<0时,写出函数图象在x轴下方所对应的自变量的范围;当y>﹣3时,写出函数值大于﹣3对应的自变量的范围.
解:
(1)∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的顶点坐标为(1,4),
当x=0时,y=x2﹣2x﹣3=﹣3,则抛物线与y轴的交点坐标为(0,﹣3),
当y=0时,x2﹣2x﹣3=0,解得x1=﹣1,x2=3,则抛物线与x轴的交点坐标为(﹣1,0),(3,0),
如图,
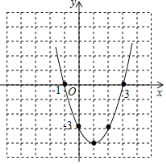
(2)由图可知,当﹣1<x<3时,y<0;
当x<0或x>1时,y>﹣3.


科目:初中数学 来源: 题型:
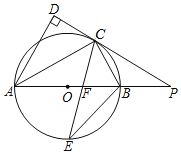
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AC平分∠DAB,直线DC与AB的延长线相交于点P,AD与PC延长线垂直,垂足为点D,CE平分∠ACB,交AB于点F,交⊙O于点E.
(1)求证:PC与⊙O相切;
(2)求证:PC=PF;
(3)若AC=8,tan∠ABC=![]() ,求线段BE的长.
,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加班长竞选,需进行演讲答辩与民主测评,民主测评时一人一票,按“优秀、良好、一般”三选一投票.如图是7位评委对小明“演讲答辩”的评分统计图及全班50位同学民主测评票数统计图.
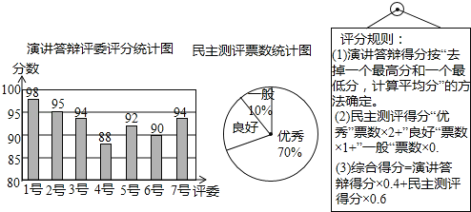
(1)求评委给小明演讲答辩分数的众数,以及民主测评为“良好”票数的扇形圆心角度数;
(2)求小明的综合得分是多少?
(3)在竞选中,小亮的民主测评得分为82分,如果他的综合得分不小于小明的综合得分,他的演讲答辩得分至少要多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A点,D点分别在x轴、y轴上,对角线BD∥x轴,反比例函数![]() 的图象经过矩形对角线的交点E,若点A(2,0),D(0,4),则k的值为( )
的图象经过矩形对角线的交点E,若点A(2,0),D(0,4),则k的值为( )

A.16B.20C.32D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低1元,每天可多售出200斤.为了保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每个人都应怀有对水的敬畏之心,从点滴做起,节水、爱水,保护我们生活的美好世界.某地近年来持续干旱,为倡导节约用水,该地采用了“阶梯水价”计费方法,具体方法:每户每月用水量不超过4吨的每吨2元;超过4吨而不超过6吨的,超出4吨的部分每吨4元;超过6吨的,超出6吨的部分每吨6元.该地一家庭记录了去年12个月的月用水量如下表,下列关于用水量的统计量不会发生改变的是( )
用水量x(吨) | 3 | 4 | 5 | 6 | 7 |
频数 | 1 | 2 | 5 | 4﹣x | x |
A. 平均数、中位数 B. 众数、中位数 C. 平均数、方差 D. 众数、方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 是
是![]() 边的中线,
边的中线,![]() 于
于![]() ,连结
,连结![]() ,点
,点![]() 在射线
在射线![]() 上(与
上(与![]() ,
,![]() 不重合)
不重合)
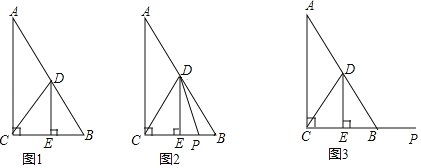
(1)如果![]()
①如图1,![]()
![]()
②如图2,点![]() 在线段
在线段![]() 上,连结
上,连结![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到线段
,得到线段![]() ,连结
,连结![]() ,补全图2猜想
,补全图2猜想![]() 、
、![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
(2)如图3,若点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() span>,连结
span>,连结![]() ,将线段
,将线段![]() 绕点逆时针旋转
绕点逆时针旋转![]() 得到线段
得到线段![]() ,连结
,连结![]() ,请直接写出
,请直接写出![]() 、
、![]() 、
、![]() 三者的数量关系(不需证明)
三者的数量关系(不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线![]() (x<0)分别交于点C(-1,2)、D(a,1).
(x<0)分别交于点C(-1,2)、D(a,1).
(1)分别求出直线及双曲线的解析式;
(2)利用图象直接写出,当x在什么范围内取值时,y1>y2.
(3)请把直线![]() 上y1<y2时的部分用黑色笔描粗一些.
上y1<y2时的部分用黑色笔描粗一些.
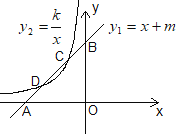
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种火爆的网红电子产品,每件产品成本![]() 元、工厂将该产品进行网络批发,批发单价
元、工厂将该产品进行网络批发,批发单价![]() (元)与一次性批发量
(元)与一次性批发量![]() (件)(
(件)(![]() 为正整数)之间满足如图所示的函数关系.
为正整数)之间满足如图所示的函数关系.
![]() 直接写出
直接写出![]() 与
与![]() 之间所满足的函数关系式,并写出自变量
之间所满足的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
![]() 若一次性批发量不超过
若一次性批发量不超过![]() 件,当批发量为多少件时,工厂获利最大?最大利润是多少?
件,当批发量为多少件时,工厂获利最大?最大利润是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com