
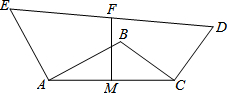
 如图,AE⊥AB,BC⊥CD,且AE=AB,BC=CD,F为DE的中点,M为AC中点,证明:FM⊥AC.
如图,AE⊥AB,BC⊥CD,且AE=AB,BC=CD,F为DE的中点,M为AC中点,证明:FM⊥AC. 分析 根据题意,作出合适的辅助线,要证FM⊥AC,只要证点M为GH的中点,FG=FH即可,要证点M为GH的中点只要证AG=CH即可,要证FG=FH,只要说明PG=QH,根据已作出的辅助线可以推出前面的结论都是正确的,从而解答本题.
解答 证明:如右图所示:
过点E作QG⊥AC交CA的延长线于点G,交HF于点Q,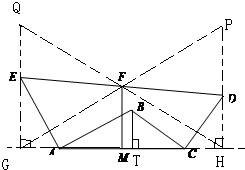
过点D作PH⊥AC交AC的延长线于点H,交GF于点P,
∴QG∥PH.
∴∠Q=∠DHF,∠EGF=∠DPF.
∵点F为DE的中点,
∴EF=DF.
在△EFQ和△DFH中,
$\left\{\begin{array}{l}{∠Q=∠DHF}\\{∠QFE=∠HFD}\\{EF=DF}\end{array}\right.$,
∴△EFQ≌△DFH(AAS).
∴QE=FD,QF=HF.
同理可证,△EFG≌△DFP.
∴EG=DP,GF=PF.
∴QG=HP.
在△QGH和△PHG中,
$\left\{\begin{array}{l}{QG=PH}\\{∠QGH=∠PHG}\\{GH=HG}\end{array}\right.$,
∴△QGH≌△PHG(SAS).
∴QH=PG.
又∵QF=HF,GF=PF,
∴FG=FH.
作BT⊥GH于点T,
∵AE⊥AB,BC⊥CD,且AE=AB,BC=CD,
∴∠EGA=∠ATB=90°,∠EAG=∠ABT.
在△AEG和△BAT中,
$\left\{\begin{array}{l}{∠EGA=∠ATB}\\{∠EAG=∠ABT}\\{AE=AB}\end{array}\right.$,
∴△AEG≌△BAT(AAS).
∴AG=BT.
同理可证,△CDH≌△BCT.
∴BT=CH.
∴AG=CH.
∵点M为AC的中点,
∴AM=MC.
∴MG=MH.
即点M为GH的中点,
∵FG=FH,
∴FM⊥AC.
点评 本题考查全等三角形的性质和判定,解题的关键是能作出合适的辅助线,根据题意用数学中的分析法进行分析,然后找出所求结论需要的条件.


科目:初中数学 来源: 题型:填空题
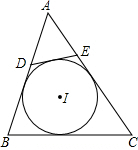 如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为21,BC边的长为6,△ADE的周长为9.
如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为21,BC边的长为6,△ADE的周长为9.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10m | B. | 20m | C. | 30m | D. | 60m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
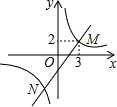 如图,一次函数y=kx-4的图象与反比例函数y=$\frac{n}{x}$的图象交于M、N两点,其中点M的坐标为(3,2),则k,n的值为( )
如图,一次函数y=kx-4的图象与反比例函数y=$\frac{n}{x}$的图象交于M、N两点,其中点M的坐标为(3,2),则k,n的值为( )| A. | 2,2 | B. | 3,8 | C. | 2,6 | D. | -2,-8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
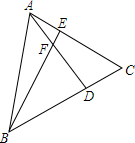 如图,在等边三角形ABC中,点E、D分别从A、C出发,沿AC,CB方向以相同的速度在线段AC,CB上运动,AD、BE相交于F点.
如图,在等边三角形ABC中,点E、D分别从A、C出发,沿AC,CB方向以相同的速度在线段AC,CB上运动,AD、BE相交于F点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
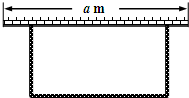 若用40m的篱笆围成一个一边靠墙的矩形场地,墙长a m,垂直于墙的边长为x m,围成的矩形场地的面积为y m2.
若用40m的篱笆围成一个一边靠墙的矩形场地,墙长a m,垂直于墙的边长为x m,围成的矩形场地的面积为y m2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com