
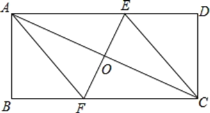
【题目】如图,在矩形ABCD中,对角线AC的垂直平分线分别交BC、AD于点F. E,垂足为O.
(1)求证:四边形AFCE为菱形;
(2)若AB=4,BC=8,求菱形AFCE的面积.
【答案】(1)详见解析;(2)20
【解析】
(1)先证明△AOE≌△COF,得出OE=OF,再根据EF垂直平分AC,可得出四边形AFCE为菱形;
(2)设AF=x,由AB=4,BC=8,得BF=8x,根据勾股定理可得出AF的长,根据菱形的面积求解即可.
(1)证明:∵EF垂直平分AC,
∴OA=OC,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠EAO=∠FCO,∠AOE=∠COF,
在△AOE和△COF中,
∠EAO=∠FOC
AO=CO
∠AOE=∠COF,
∴△AOE≌△COF,
∴OE=OF,
∴四边形AFCE为菱形;
(2)解:设AF=x,
∵AB=4,BC=8,∴BF=8x,
∴AF2=AB2+BF2,
∴x2=42+(8x)2,
∴x=5,
∴S菱形AFCE=FCAB=5×4=20,
∴菱形面积为20.


科目:初中数学 来源: 题型:
【题目】德州扒鸡闻名全国,远销海外,被誉为“天下第一鸡”.某种德州扒鸡其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售量可增加20千克,若该专卖店销售这种扒鸡想要平均每天获利2240元,请回答:
(1)每千克这种扒鸡应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,贏得市场,该店应按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b的图象与反比例函数![]() 的图象交于点A(-2,-5),C(n,2),交y轴于点B,交x轴于点D.
的图象交于点A(-2,-5),C(n,2),交y轴于点B,交x轴于点D.
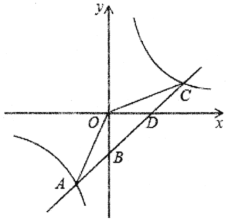
(1)求反比例函数![]() 和一次函数y=kx+b的表达式;
和一次函数y=kx+b的表达式;
(2)请直接写出不等式![]() 的解集.
的解集.
(3)连接OA,OC.求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=(x-a)(x-3)(0<a<3)的图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点D,过其顶点C作直线CP⊥x轴,垂足为点P,连接AD、BC.
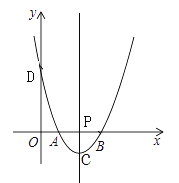
(1)求点A、B、D的坐标;
(2)若△AOD与△BPC相似,求a的值;
(3)点D、O、C、B能否在同一个圆上,若能,求出a的值,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若B、P在直线a的异侧, BM直线a于点M,CN直线a于点N,连接PM、PN;
 (1) 延长MP交CN于点E(如图2)。 求证:△BPM△CPE; 求证:PM = PN;
(1) 延长MP交CN于点E(如图2)。 求证:△BPM△CPE; 求证:PM = PN;
(2) 若直线a绕点A旋转到图3的位置时,点B、P在直线a的同侧,其它条件不变。此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3) 若直线a绕点A旋转到与BC边平行的位置时,其它条件不变。请直接判断四边形MBCN
的形状及此时PM=PN还成立吗?不必说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某货站传送货物的平面示意图,AD与地面的夹角为60°,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°变成37°,因此传送带的落地点由点B到点C向前移动了2米.

(1)求点A与地面的高度;
(2)如果需要在货物着地点C的左侧留出2米,那么请判断距离D点14米的货物2是否需要挪走,并说明理由.(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
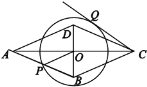
【题目】如图,菱形ABCD中,对角线AC和BD相交于点O,AC=10,BD=4,动点P在边AB上运动,以点O为圆心,OP为半径作⊙O,CQ切⊙O于点Q,则在点P运动过程中,CQ的长的最大值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的直径,以A为圆心,弦AB为半径画弧交⊙O于点C,连结BC交AD于点E,若DE=3,BC=8,则⊙O的半径长为( )

A.![]() B.5C.
B.5C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】取三张形状大小一样,质地完全的相同卡片,在三张卡片上分别写上“李明、王强、孙伟”这三个同学的名字,然后将三张卡片放入一个不透明的盒子里.
(1)林老师从盒子中任取一张,求取到写有李明名字的卡片概率是多少?
(2)林老师从盒子中取出一张卡片,记下名字后放回,再从盒子中取出第二张卡片,记下名字.用列表或画树形图列出林老师取到的卡片的所有可能情况,并求出两次都取到写有李明名字的卡片的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com