
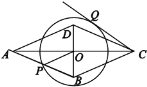
【题目】如图,菱形ABCD中,对角线AC和BD相交于点O,AC=10,BD=4,动点P在边AB上运动,以点O为圆心,OP为半径作⊙O,CQ切⊙O于点Q,则在点P运动过程中,CQ的长的最大值为_______.
 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
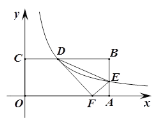
【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B 的坐标为(8,4),反比例函数y=![]() (k>0)的图象分别交边BC、AB 于点D、E,连结DE,△DEF与△DEB关于直线DE对称,当点F恰好落在线段OA上时,则k的值是________.
(k>0)的图象分别交边BC、AB 于点D、E,连结DE,△DEF与△DEB关于直线DE对称,当点F恰好落在线段OA上时,则k的值是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
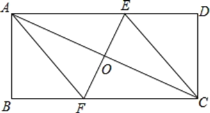
【题目】如图,在矩形ABCD中,对角线AC的垂直平分线分别交BC、AD于点F. E,垂足为O.
(1)求证:四边形AFCE为菱形;
(2)若AB=4,BC=8,求菱形AFCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某次商业足球比赛中,门票销售单位对团体购买门票实行优惠,决定在原定票价基础上每张降价100元,这样按原定票价需花费14 000元购买的门票张数,现在只花费了10 500元.
(1)求每张门票的原定票价;
(2)根据实际情况,组织单位决定对于个人购票也采取优惠措施,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】芜湖市某医院计划选购A,B两种防护服.已知A防护服每件价格是B防护服每件价格的2倍,用80000元单独购买A防护服比用80000元单独购买B防护服要少50件.如果该医院计划购买B防护服的件数比购买A防护服件数的2倍多8件,且用于购买A,B两种防护服的总经费不超过320000元,那么该医院最多可以购买多少件B防护服?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )

A. ﹣2<m<![]() B. ﹣3<m<﹣
B. ﹣3<m<﹣![]() C. ﹣3<m<﹣2 D. ﹣3<m<﹣
C. ﹣3<m<﹣2 D. ﹣3<m<﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图,矩形![]() 是矩形
是矩形![]() 的“减半”矩形.
的“减半”矩形.
请你解决下列问题:
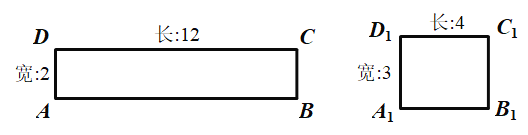
(1)当矩形的长和宽分别为![]() ,
,![]() 时,它是否存在“减半”矩形?请作出判断,并说明理由.
时,它是否存在“减半”矩形?请作出判断,并说明理由.
(2)边长为![]() 的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,请说明理由.
的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com