
【题目】如图,在平面直角坐标系中,二次函数y=(x-a)(x-3)(0<a<3)的图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点D,过其顶点C作直线CP⊥x轴,垂足为点P,连接AD、BC.
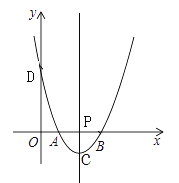
(1)求点A、B、D的坐标;
(2)若△AOD与△BPC相似,求a的值;
(3)点D、O、C、B能否在同一个圆上,若能,求出a的值,若不能,请说明理由.
【答案】(1)(1)A(a,0),B(3,0),D(0,3a).(2)a的值为![]() .(3)当a=
.(3)当a=![]() 时,D、O、C、B四点共圆.
时,D、O、C、B四点共圆.
【解析】(1)根据二次函数的图象与x轴相交,则y=0,得出A(a,0),B(3,0),与y轴相交,则x=0,得出D(0,3a).
(2)根据(1)中A、B、D的坐标,得出抛物线对称轴x=![]() ,AO=a,OD=3a,代入求得顶点C(
,AO=a,OD=3a,代入求得顶点C(![]() ,-
,-![]() ),从而得PB=3-
),从而得PB=3- ![]() =
=![]() ,PC=
,PC=![]() ;再分情况讨论:①当△AOD∽△BPC时,根据相似三角形性质得
;再分情况讨论:①当△AOD∽△BPC时,根据相似三角形性质得 ,解得:a=
,解得:a= ![]() 3(舍去);
3(舍去);
②△AOD∽△CPB,根据相似三角形性质得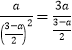 ,解得:a1=3(舍),a2=
,解得:a1=3(舍),a2=![]() ;
;
(3)能;连接BD,取BD中点M,根据已知得D、B、O在以BD为直径,M(![]() ,
,![]() a)为圆心的圆上,若点C也在此圆上,则MC=MB,根据两点间的距离公式得一个关于a的方程,解之即可得出答案.
a)为圆心的圆上,若点C也在此圆上,则MC=MB,根据两点间的距离公式得一个关于a的方程,解之即可得出答案.
(1)∵y=(x-a)(x-3)(0<a<3)与x轴交于点A、B(点A在点B的左侧),
∴A(a,0),B(3,0),
当x=0时,y=3a,
∴D(0,3a);
(2)∵A(a,0),B(3,0),D(0,3a).∴对称轴x=![]() ,AO=a,OD=3a,
,AO=a,OD=3a,
当x= ![]() 时,y=-
时,y=- ![]() ,
,
∴C(![]() ,-
,-![]() ),
),
∴PB=3-![]() =
=![]() ,PC=
,PC=![]() ,
,
①当△AOD∽△BPC时,
∴![]() ,
,
即  ,
,
解得:a= ![]() 3(舍去);
3(舍去);
②△AOD∽△CPB,
∴![]() ,
,
即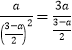 ,
,
解得:a1=3(舍),a2=![]() .
.
综上所述:a的值为![]() ;
;
(3)能;连接BD,取BD中点M,
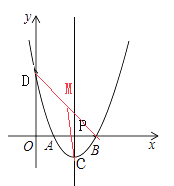
∵D、B、O三点共圆,且BD为直径,圆心为M(![]() ,
,![]() a),
a),
若点C也在此圆上,
∴MC=MB,
∴ ,
,
化简得:a4-14a2+45=0,
∴(a2-5)(a2-9)=0,
∴a2=5或a2=9,
∴a1=![]() ,a2=-
,a2=-![]() ,a3=3(舍),a4=-3(舍),
,a3=3(舍),a4=-3(舍),
∵0<a<3,
∴a=![]() ,
,
∴当a=![]() 时,D、O、C、B四点共圆.
时,D、O、C、B四点共圆.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
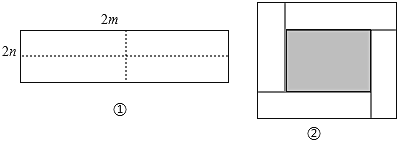
【题目】如图![]() 所示是一个长为2m,宽为
所示是一个长为2m,宽为![]() 的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图2的方式拼成一个正方形
的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图2的方式拼成一个正方形
![]() 如图
如图![]() 中的阴影部分的正方形的边长等于______
中的阴影部分的正方形的边长等于______![]() 用含m、n的代数式表示
用含m、n的代数式表示![]() ;
;
![]() 请用两种不同的方法列代数式表示图
请用两种不同的方法列代数式表示图![]() 中阴影部分的面积:
中阴影部分的面积:
方法![]() :______;
:______;
方法![]() :______;
:______;
![]() 观察图
观察图![]() ,试写出
,试写出![]() 、
、![]() 、mn这三个代数式之间的等量关系:______;
、mn这三个代数式之间的等量关系:______;
![]() 根据
根据![]() 题中的等量关系,若
题中的等量关系,若![]() ,
,![]() ,求图
,求图![]() 中阴影部分的面积.
中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,小明和父母一起开车到距家200千米的景点旅游.出发前,汽车油箱内储油45升;当行驶150千米时,发现油箱剩余油量为30升.
(1)已知油箱内余油量y(升)是行驶路程x(千米)的一次函数,求y与x的函数关系式;
(2)当油箱中余油量少于3升时,汽车将自动报警.如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有2部不同的电影A、B,甲、乙、丙3人分别从中任意选择1部观看.
(1)求甲选择A部电影的概率;
(2)求甲、乙、丙3人选择同一部电影的概率(请用画树状图的方法给出分析过程,并求出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7,
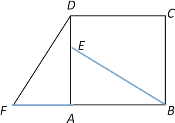
求:(1)指出旋转中心和旋转角度
(2)求DE的长度
(3)BE与DF的位置关系如何?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在上海的小明一家将于5月1日到苏州进行自驾游,准备将行程分为上午和下午,上午的备选地点为:A-重元寺、B-苏州乐园、C-观前街,下午的备选地点为:D-李公堤、E-金鸡湖摩天轮公园.
(1)请用画树状图或列表的方法写出小明家所有可能的游玩方式(用字母表示即可);
(2)求小明一家恰好整天在工业园区游玩的概率.(提示:重元寺、李公堤、金鸡湖摩天轮公园在工业园区)
查看答案和解析>>
科目:初中数学 来源: 题型:
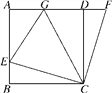
【题目】如图,在正方形ABCD中,E是AB边上一点,F是AD延长线上一点,BE=DF.
(1)求证:CE=CF;
(2)若点G在AD边上,且∠GCE=45°,BE=3,DG=5,求GE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
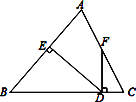
【题目】如图所示,△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于F.
⑴若∠AFD=155°,求∠EDF的度数;
⑵若点F是AC的中点,求证:∠CFD=![]() ∠B.
∠B.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段MN=10cm,点C是直线MN上一点,NC=4cm,若P是线段MN的中点,Q是线段NC的中点,则线段PQ的长度是( )
A.7cmB.7cm或3cmC.5cmD.3cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com