
分析 (1)先算零指数幂、负整数指数幂和平方,再计算加减法即可求解;
(2)把(p-q)看作一个整体,再根据同底数幂的乘除法法则计算即可求解;
(3)先算同底数幂的乘法、积的乘方、同底数幂的除法,再合并同类项即可求解;
(4)先算幂的乘方和积的乘方,再根据同底数幂的乘除法计算法则计算即可求解.
解答 解:(1)${({π-1})^0}-{({-\frac{1}{2}})^{-1}}-{2^2}$
=1+2-4
=-1;
(2)(p-q)4÷(q-p)3•(p-q)2
=-(p-q)4-3+2
=-(p-q)3;
(3)a•a2•a3+(-2a3)2-a8÷a2
=a6+4a6-a6
=4a6;
(4)(-2x)2•(x2)3÷(-x)2
=4x2•x6÷x2
=4x6.
点评 考查了整式的混合运算,“整体”思想在整式运算中较为常见,适时采用整体思想可使问题简单化,并且迅速地解决相关问题,此时应注意被看做整体的代数式通常要用括号括起来.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题
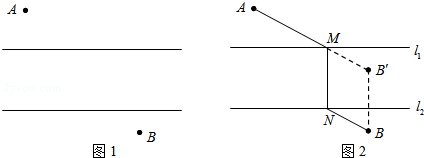
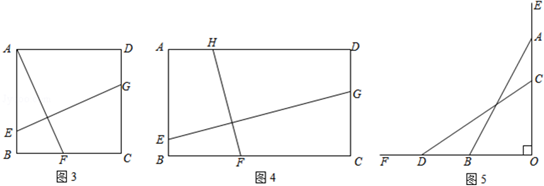
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{1-a}$ | B. | $\sqrt{1-a}$ | C. | -$\sqrt{a-1}$ | D. | $\sqrt{a-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com