
分析 (1)一般用增长后的量=增长前的量×(1+增长率),2015年要投入教育经费是2500(1+x)万元,在2015年的基础上再增长x,就是2016年的教育经费数额,即可列出方程求解.
(2)利用(1)中求得的增长率来求2017年该地区将投入教育经费.
解答 解:设增长率为x,根据题意2015年为2500(1+x)万元,2016年为2500(1+x)2万元.
则2500(1+x)2=3600,
解得x=0.2=20%,或x=-2.2(不合题意舍去).
答:这两年投入教育经费的平均增长率为20%.
(2)3600×(1+20%)=4320(万元).
故根据(1)所得的年平均增长率,预计2017年该地区将投入教育经费4320万元.
点评 本题考查了一元二次方程中增长率的知识.增长前的量×(1+年平均增长率)年数=增长后的量.


科目:初中数学 来源: 题型:填空题
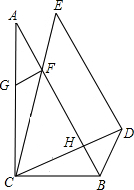 如图,Rt△ABC和Rt△CDE中,∠A=30°,∠E=45°,AB=CE,∠BCD=30°,FG⊥AB,下列结论:①CH=FH;②BC=GC;③四边形BDEF为平行四边形;④FH=GF+BH.其中正确的结论是①②④(填序号).
如图,Rt△ABC和Rt△CDE中,∠A=30°,∠E=45°,AB=CE,∠BCD=30°,FG⊥AB,下列结论:①CH=FH;②BC=GC;③四边形BDEF为平行四边形;④FH=GF+BH.其中正确的结论是①②④(填序号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $9\sqrt{2}$ | B. | $3\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $3\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
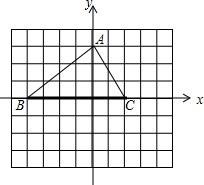 如图,△ABC的顶点分别为A(0,3),B(-4,0),C(2,0),且△BCD与△ABC全等,则点D坐标可以是( )
如图,△ABC的顶点分别为A(0,3),B(-4,0),C(2,0),且△BCD与△ABC全等,则点D坐标可以是( )| A. | (-2,-3) | B. | (2,-3) | C. | (2,3) | D. | (0,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com