
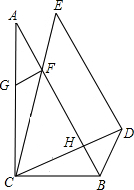
 如图,Rt△ABC和Rt△CDE中,∠A=30°,∠E=45°,AB=CE,∠BCD=30°,FG⊥AB,下列结论:①CH=FH;②BC=GC;③四边形BDEF为平行四边形;④FH=GF+BH.其中正确的结论是①②④(填序号).
如图,Rt△ABC和Rt△CDE中,∠A=30°,∠E=45°,AB=CE,∠BCD=30°,FG⊥AB,下列结论:①CH=FH;②BC=GC;③四边形BDEF为平行四边形;④FH=GF+BH.其中正确的结论是①②④(填序号). 分析 求出∠ABC=60°,又∠BCD=30°,得到∠AHC为直角,由Rt△CDE中,∠E=45°,得到∠ECD=45°,△FCH为等腰直角三角形,得到FH=CH,选项①正确;
过G作GM于CD垂直,交CD于M,证出四边形GMHF为矩形,根据矩形的对边相等,得到GF=MH,GM=FH,得到GM=CH,由一对直角相等,再根据同角的余角相等得到一对角相等,利用ASA得到△CGM与△CBH全等,得到CG=CB,选项②正确;
根据全等得到GM=CH,由FH=CH=CM+MH,得到选项④正确;
要使四边形FBDE为平行四边形,由一对直角即同位角相等,得到BF与DE平行,还要使EC与DB平行,故要使同旁内角互补,即要∠HBD为45°,而∠HBD不一定为45°,故选项③不一定成立;即可得出结论.
解答 解:∵Rt△ABC中,∠A=30°,
∴∠ABC=60°,又∠BCD=30°,
∴∠FHC=90°,
又Rt△CDE中,∠E=45°,
∴∠ECD=45°,
∴△FCH为等腰直角三角形,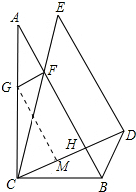
∴FH=HC,故选项①正确;
过G作GM⊥CD,交CD于M,如图所示:
∴∠GMD=90°,
∴∠GCM+∠CGM=90°,又∠ACB=90°
∴∠GCM+∠BCH=90°,
∴∠CGM=∠BCH,
∵∠FHM=90°(已证),又GF⊥AB,
∴∠GFH=90°,
∴四边形GMHF为矩形,
∴GM=FH,GF=MH,
又FH=CH,
∴GM=CH,
在△GCM和△CBH中,$\left\{\begin{array}{l}{∠GMC=∠CHB}&{\;}\\{GM=CH}&{\;}\\{∠CGM=∠BCH}&{\;}\end{array}\right.$,
∴△GCM≌△CBH(AAS),
∴CM=BH,BC=CG,故选项②正确;
∴FH=CH=CM+MH=BH+GF,故选项④正确;
∵∠AHC=∠EDC=90°,
∴FB∥ED,
要使四边形BDEF为平行四边形,还需BD∥EC,
即要∠FCB+∠CBD=180°,
而∠FCB=∠ECD+∠DCB=45°+30°=75°,
故要∠CBD=∠CBA+∠ABD=105°,又∠CBA=60°,
即要∠ABD=45°,而∠ABD不一定等于45°,
故选项③不一定成立,
则其中正确的结论有①②④.
故答案为:①②④.
点评 此题考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,以及平行四边形的判定等知识.本题综合性强,有一定难度,属于结论型开放题,作出辅助线GM构造全等三角形是本题的突破点.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com