
����Ŀ�����ı���OABC�У�AB��OC��BC��x����C��A��1��-1����B��3��-1��������P��O���������x����������2����λ/����ٶ��˶�����P��PQ��OA��Q����P���˶���ʱ��Ϊt�루0 < t < 2������OPQ���ı���OABC�ص������ΪS��
��1����O��A��B����������ߵĽ���ʽ��ȷ������M�����ꣻ
��2���ú�t�Ĵ���ʽ��ʾP��Q��������ꣻ
��3������OPQ��P����ʱ����ת90�����Ƿ����t��ʹ����OPQ�Ķ���O��Q�����������ϣ������ڣ�ֱ��д��t��ֵ���������ڣ���˵�����ɣ�
��4����S��t�ĺ�������ʽ��

���𰸡���1��![]() ����M
����M![]() ��2��
��2��![]() ��3��
��3��![]() ��
��![]() ��4����
��4����![]() ʱ��
ʱ�� ![]() ��
��![]() ʱ��
ʱ�� ![]() ��
��![]() ʱ��
ʱ�� ![]()
�������������������1���������ߵĽ���ʽΪy=ax2+bx+c��a��0����Ȼ�����A��B������������a��b��ֵ���õ�����ʽ��Ȼ����ݶ���ʽ���䷽Ϊ����ʽ�㼴�ɣ�
��2������P���ٶ����OP�����ɵõ���P�����꣬�ٸ��ݵ�A�����������AOC=45�㣬Ȼ���жϳ���POQ�ǵ���ֱ�������Σ����ݵ���ֱ�������ε��������Q������꼴�ɣ�
��3��������ת���������O��Q�����꣬Ȼ��ֱ���������߽���ʽ������⣻
��4�������Q���A�غ�ʱ��t=1����P���C�غ�ʱ��t=1.5��t=2��PQ������B��Ȼ��֢�0��t��1ʱ���ص����ֵ�������ڡ�POQ��������ڵ�1��t��1.5ʱ���ص����ֵ����������������ֱ�������ε�����IJ��1.5��t��2ʱ���ص����ֵ�����������ε������ȥһ������ֱ�������ε�������ֱ���ʽ��������Ϊ���.
�����������1��![]() ����M
����M![]()
![]()
��2��![]()
��3��![]() ��
��![]()
��4����![]() ʱ��
ʱ�� ![]()
��![]() ʱ��
ʱ�� ![]()
��![]() ʱ��
ʱ�� ![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��ȫУѧ��������������֪ʶ���ԣ�Ϊ���˽���Խ���������ȡ����ѧ���ijɼ����з��������ɼ���Ϊ�����ȼ������ϸ�һ�㡢���㣬�����Ƴ���������ͳ��ͼ���������ͼ����������Ϣ����������⣺ 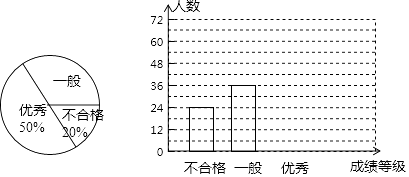
��1���뽫��������ͳ��ͼ����������
��2����һ�㡱�ȼ��������ε�Բ�ĽǵĶ������ȣ�
��3������һ�㡱�͡����㡱������Ϊ���ɼ�����Уѧ����1200�ˣ�������ƴ˴β����У�ȫУ����ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=12cm��BC=24cm��������þ����ضԽ���BD�۵�����ôͼ����Ӱ���ֵ������ ��cm2 �� 
A.72
B.90
C.108
D.144
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��OΪֱ��AB��һ�㣬����O������OC����AOC=30�㣬��һֱ�����ǰ壨��M=30�㣩��ֱ�Ƕ�����ڵ�O����һ��ON������OA�ϣ���һ��OM��OC����ֱ��AB���Ϸ���
��1����ͼ1�е����ǰ��Ƶ�O��ÿ��3����ٶ���˳ʱ�뷽����תһ�ܣ���ͼ2������t���OMǡ��ƽ�֡�BOC������t��ֵ���ڴ�ʱON�Ƿ�ƽ�֡�AOC����˵�����ɣ�
��2���ڣ�1���ʵĻ����ϣ������ǰ���ת����ͬʱ������OCҲ��O����ÿ��6����ٶ���˳ʱ�뷽����תһ�ܣ���ͼ3����ô�����ʱ��OCƽ�֡�MON����˵�����ɣ�
��3���ڣ�2���ʵĻ����ϣ������ʱ��OCƽ�֡�MOB���뻭ͼ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ĸijУ������չУ���γ̽��裬�ƻ���������ѧ���͡�������ѧʵ�顱���������赸���͡��ֹ���֯���ȶ�����ţ�Ҫ��ÿλѧ��������ѡ������һ�����ţ�Ϊ�ˣ���������˱�У���꼶����ѧ��ѡ�����ŵ����������������Ƴ�����ͳ��ͼ��������������
ijУ������ѧ��ѡ����������ͳ�Ʊ�
ѡ������ | ��ռ�ٷֱ� |
��ѧ���� | a |
��ѧʵ�� | 35% |
�����赸 | b |
�ֹ���֯ | 10% |
���� | c |
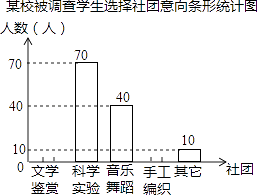
����ͳ��ͼ���е���Ϣ������������⣺
��1���ε����ѧ����������a��b��c��ֵ��
��2��������ͳ��ͼ����������
��3������У����1200��ѧ�����Թ���ȫУѡ��ѧʵ�顱���ŵ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ͯ��A����ţ�������C����A��C���Ӱ�L�ľ���ֱ�ΪAB=2km��CD=4km�ң�BD=8km�� 
��1����ͯ��A����ţǣ���ӱ�P����ˮ���ٻص���C����ȷ��P�ںδ�������·����̣�����ͼ�л�����ˮ��λ�ã�������ͼ�ۼ�����
����˵�����ɣ�
��2�������1���е����·�̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ��ѧ���ӵ�A��ƫ��60��������40�ף������B���ٴ�B�ر�ƫ��30�������������ף������C����ʱǡ���ڵ�A����������������˵����ȷ���ǣ�������
A. ��A��BC�ľ���Ϊ30��
B. ��B�ڵ�C����ƫ��60������
C. ��A�ڵ�B����ƫ��60������30�״�
D. ���϶�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A�������϶�Ӧ����Ϊa����B��Ӧ����Ϊb����a��b����|a+3|+��b��2��2=0��
��1����A��B����Ķ�Ӧ����a��b��
��2����C�������϶�Ӧ����Ϊx����x�Ƿ���2x+1= ![]() x��8�Ľ�.
x��8�Ľ�.
�����߶�BC�ij���
�����������Ƿ���ڵ�P��ʹPA+PB=BC�������P��Ӧ�������������ڣ�˵�����ɣ�![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com