Question

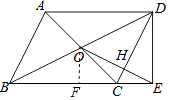
【题目】如图，ABCD的对角线相交于点O，将线段OD绕点O旋转，使点D的对应点落在BC延长线上的点E处，OE交CD于H，连接DE．

（1）求证：DE⊥BC；
（2）若OE⊥CD，求证：2CEOE=CDDE；
（3）若OE⊥CD，BC=3，CE=1，求线段AC的长．

Answer 1

【答案】
（1）

证明：由旋转可知OE=OD，

∴∠ODE=∠OED，

∵四边形ABCD是平行四边形，

∴OB=OD，OA=OC

∴OB=OE，

∴∠OEB=∠OBE，

∵∠BDE+∠DBE+∠BED=180°，

∴∠ODE+∠OED+∠OEB+∠OBE=180°

∴∠OED+∠OEB=90°，

即∠DEB=90°，

∴DE⊥BC；

（2）

解：∵OE⊥CD，

∴∠CHE=90°，

∴∠CDE+∠OED=90°

∵∠OED+∠OEB=90°，

∴∠CDE=∠OEB

∵∠OEB=∠OBE，

∴∠CDE=∠OBE，

∵∠CDE=∠OBE，∠CED=∠DEB，

∴△CDE∽△DBE

∴ = ，即CEBD=CDDE，

∵OE=OD，OB=OD，BD=OB+OD，

∴BD=2OE，

∴2CEOE=CDDE；

（3）

解：∵BC=3，CE=1，

∴BE=4

由（2）知，△CDE∽△DBE

∴ = ，即DE2=CEBE=4，

∴DE=2，

过点O作OF⊥BE，垂足为F，

∵OB=OE，

∴BF=EF= BE=2，

∴CF=EF﹣CE=1

∵OB=OD，BE=EF，

∴OF= DE=1，

在Rt△OCF中，OC= = = ，

∴AC=2OC=2 ．

【解析】（1）由旋转的性质得到OE=OD，根据等腰三角形的性质得到∠ODE=∠OED，根据平行四边形的性质得到OB=OD，OA=OC等量代换得到OB=OE，推出∠DEB=90°，根据垂直的定义得到结论；（2）由垂直的定义得到∠CHE=90°，根据余角的性质得到∠CDE=∠OEB等量代换得到∠CDE=∠OBE，根据相似三角形的性质得到CEBD=CDDE，等量代换即可得到结论；（3）根据相似三角形的性质得到DE2=CEBE=4，求得DE=2，过点O作OF⊥BE，垂足为F，根据等腰三角形的想知道的BF=EF= BE=2，根据勾股定理即可得到结论．
【考点精析】掌握勾股定理的概念和平行四边形的性质是解答本题的根本，需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．