
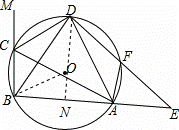
在△ABC的外接圆⊙O中,△ABC的外角平分线CD交⊙O于点D,F为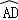 上﹣
上﹣
点,且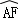 =
=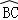 连接DF,并延长DF交BA的延长线于点E.
连接DF,并延长DF交BA的延长线于点E.
(1)判断DB与DA的数量关系,并说明理由;
(2)求证:△BCD≌△AFD;
(3)若∠ACM=120°,⊙O的半径为5,DC=6,求DE的长.
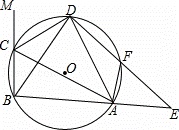
解:(1)DB=DA.
理由:∵CD是△ABC的外角平分线,
∴∠MCD=∠ACD,
∵∠MCD+∠BCD=180°,∠BCD+∠BAD=180°,
∴∠MCD=∠BAD,
∴∠ACD=∠BAD,
∵∠ACD=∠ABD,
∴∠ABD=∠BAD,
∴ DB=DA;
DB=DA;
(2)证明:∵DB=DA,
∴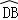 =
=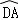 ,
,
∵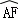 =
=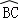 ,
,
∴AF=BC,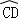 =
=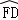 ,
,
∴CD=FD,
在△BCD和△AFD中,
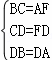 ,
,
∴△BCD≌△AFD(SSS);
(3)连接DO并延长,交AB于点N,连接OB,
∵DB=DA,
∴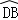 =
=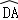 ,
,
∴DN⊥AB,
∵∠ACM=120°,
∴∠ABD=∠ACD=60° ,
,
∵DB=DA,
∴△ABD是等边三角形,
∴∠OBA=30°,
∴ON=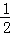 OB=
OB=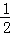 ×5=2.5,
×5=2.5,
∴DN=ON+OD=7.5,
∴BD=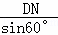 =5
=5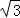 ,
,
∴AD=BD=5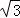 ,
,
∵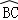 =
=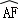 ,
,
∴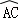 =
=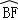 ,
,
∴∠ADC=∠BDF,
∵∠ABD=∠ACD,
∴△ACD∽△EBD,
∴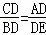 ,
,
∴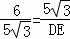 ,
,
∴DE=12.5.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
图1是某中学九年级一班全体学生对三种水果喜欢人数的频数分布 统计图,根据图中信息回答下列问题:
统计图,根据图中信息回答下列问题:
(1)九年级一班总人数是多少人?
(2)喜欢哪种水果人数的频数最低?并求出该频率;
(3)请根据频数分布统计图(图1)的数据,补全扇形统计图(图2);
(4)某水果摊位上正好只摆放有这三种水果出售,王阿姨去购买时,随机购买其中两种水果,恰好买到樱桃和枇杷的概率是多少?用树状图或列表说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
达州市某中学举行了“中国梦,中国好少年”演讲比赛,菲菲同学将选手成绩划分为A、B、C、D四个等级,绘制了两种不完整统计图.
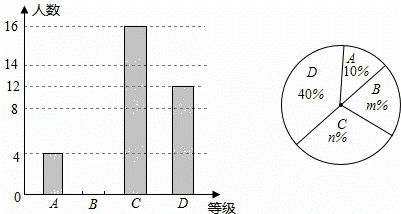
根据图中提供的信息,解答下列问题:
(1)参加演讲比赛的学生共有 人,扇形统计图中m= ,n= ,并把条形统计图补充完整.
(2)学校欲从A等级2名男生2名女生中随机选取两人,参加达州市举办的演讲比赛,请利用列表法或树状图,求A等级中一男一女参加比赛的概率.(男生分别用代码 A1、A2表示,女生分别用代码B1、B2表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读理解:
如图①,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=900,那么我们把这样的四边形叫做“完美筝形”。
将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示的形状, 再展开得到图③,其中CE、CF为折痕,∠BCD=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB′、FD′相交于点O。
再展开得到图③,其中CE、CF为折痕,∠BCD=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB′、FD′相交于点O。
简单应用:
(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是 ;
(2)当图③中的∠BCD=1200时,∠AEB′= 0 ;
;
(3)当图②中的四边形AECF为菱形时,对应图③中的“ 完美筝形”有 个(包含四边形ABCD)
拓展提升:
当图中的∠BCD=900时,连接AB′,请探求∠AB′E的度数,并说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com