
【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC,BD于点E,P,连接OE,∠ADC=60°,![]() ,则下列结论:①∠CAD=30°②
,则下列结论:①∠CAD=30°②![]() ③
③![]() ④
④![]() ,正确的个数是______________
,正确的个数是______________

【答案】①②③④
【解析】
①先根据角平分线和平行得:∠BAE=∠BEA,则AB=BE=1,由有一个角是60°的等腰三角形是等边三角形得:△ABE是等边三角形,由外角的性质和等腰三角形的性质得:∠ACE=30°,最后由平行线的性质可作判断;
②先根据三角形中位线定理得:OE=![]() AB=
AB=![]() ,OE∥AB,根据勾股定理计算OC=
,OE∥AB,根据勾股定理计算OC=![]() 和OB的长,可得BD的长;③因为∠BAC=90°,根据平行四边形的面积公式可作判断;④根据三角形中位线定理及直角三角形30°角的性质可作判断.
和OB的长,可得BD的长;③因为∠BAC=90°,根据平行四边形的面积公式可作判断;④根据三角形中位线定理及直角三角形30°角的性质可作判断.
解:①∵AE平分∠BAD,
∴∠BAE=∠DAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠ABC=∠ADC=60°,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴△ABE是等边三角形,
∴AE=BE=1,
∵BC=2,
∴EC=1,
∴AE=EC,
∴∠EAC=∠ACE,
∵∠AEB=∠EAC+∠ACE=60°,
∴∠ACE=30°,
∵AD∥BC,
∴∠CAD=∠ACE=30°,
故①正确;
②∵BE=EC,OA=OC,
∴OE=![]() AB=
AB=![]() ,OE∥AB,
,OE∥AB,
∴∠EOC=∠BAC=60°+30°=90°,
Rt△EOC中,OC=![]() ,
,
∴OA=OC=![]() ,
,
Rt△OAB中,OB=![]() ,
,
∴BD=2OB=![]() ,
,
故②正确;
③由②知:∠BAC=90°,
∴SABCD=ABAC,
故③正确;
④由②知:OE是△ABC的中位线,
∴OE=![]() AB,
AB,
∵∠BAC=90°,∠ACB=30°,
∴AB=![]() BC=
BC=![]() AD,
AD,
∴![]() ,
,
故④正确;
本题正确的有:①②③④,4个,
故答案为:①②③④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的面积为20cm2,对角线相交于点O.以AB、AO为邻边画平行四边形AOC1B,对角线相交于点O ;以AB、AO 为邻边画平行四边形AO1C2B,对角线相交于点O2 :……以此类推,则平行四边形AO4C5B的面积为( )

A.![]() cm2B.
cm2B.![]() cm2C.
cm2C.![]() cm2D.
cm2D. ![]() cm2
cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:基本不等式![]() ≤
≤![]() (a>0,b>0),当且仅当a=b时,等号成立.其中我们把
(a>0,b>0),当且仅当a=b时,等号成立.其中我们把![]() 叫做正数a、b的算术平均数,
叫做正数a、b的算术平均数,![]() 叫做正数a、b的几何平均数,它是解决最大(小)值问题的有力工具.
叫做正数a、b的几何平均数,它是解决最大(小)值问题的有力工具.
例如:在x>0的条件下,当x为何值时,x+![]() 有最小值,最小值是多少?
有最小值,最小值是多少?
解:∵x>0,![]() >0∴
>0∴![]() ≥
≥![]() 即是x+
即是x+![]() ≥2
≥2![]()
∴x+![]() ≥2
≥2
当且仅当x=![]() 即x=1时,x+
即x=1时,x+![]() 有最小值,最小值为2.
有最小值,最小值为2.
请根据阅读材料解答下列问题
(1)若x>0,函数y=2x+![]() ,当x为何值时,函数有最小值,并求出其最小值.
,当x为何值时,函数有最小值,并求出其最小值.
(2)当x>0时,式子x2+1+![]() ≥2成立吗?请说明理由.
≥2成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过点(0,-3).
的图象经过点(0,-3).
(1)求这个二次函数的函数解析式;
(2)当x取何值时,函数y的值随着x的增大而增大;
(3)当x取何值时,函数的值为0.
查看答案和解析>>
科目:初中数学 来源: 题型:
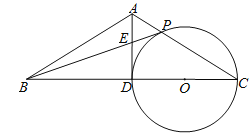
【题目】已知:如图,在△ABC中,AB=AC,点D是边BC的中点,以CD为直径作⊙O,交边AC于点P,连接BP,交AD于点E.
(1)求证:AD是⊙O的切线;
(2)如果PB是⊙O的切线,BC=4,求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
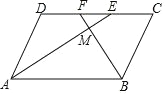
【题目】如图,在 ABCD 中,AE、BF 分别平分∠DAB 和∠ABC,交 CD 于点 E、F,AE、BF 相交于点 M.
(1)求证:AE⊥BF;
(2)判断线段 DF 与 CE 的大小关系,并予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个涵洞成抛物线形,它的截面如图,现测得:当水面宽AB=1.6 m时,涵洞顶点与水面的距离为2.4 m,离开水面1.5 m处是涵洞宽ED.
(1)求抛物线的解析式;
(2)求ED的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级某班部分学生植树,若每人平均植树8棵,还剩7棵;若每人植树9棵,则有一名学生植树的棵树多于3棵而小于6棵.若设学生人数为x人,则植树棵树为(8x7)人,则下面给出的不等式(组)中,能准确求出学生人数与种植树木数量的是( )
A.8x769(x1)B.8x739(x1)
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
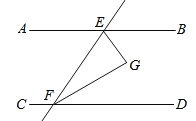
【题目】如图,直线AB∥CD,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,
(1)若∠AEF=50°,求∠EFG的度数.
(2)判断EG与FG的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com