
分析 (1)把方程左边分解得到(x-1)(x-2)=0,则原方程可化为x-1=0或x-2=0,然后解两个一次方程即可.
(2)把常数项移到右边,两边加上一次项系数一半的平方,左边配成完全平方的形式,再用直接开平方求出方程的根.
解答 解:(1)x2-3x+2=0;
分解因式得:(x-1)(x-2)=0,
∴x-1=0,x-2=0,
∴x1=1,x2=2.
(2)x2-6x+4=0.
x2-6x=-4
x2-6x+9=5
(x-3)2=5
x-3=±$\sqrt{5}$
∴x=3$±\sqrt{5}$
∴x1=3$+\sqrt{5}$,x2=3-$\sqrt{5}$.
点评 本题考查了解一元二次方程的应用,解此题的关键是能把一元二次方程转化成一元一次方程.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| 学生平均身高(单位:m) | 标准差 | |
| 八(1)班 | 1.57 | 0.3 |
| 八(2)班 | 1.57 | 0.7 |
| 八(3)班 | 1.60 | 0.3 |
| 八(4)班 | 1.60 | 0.7 |
| A. | 八(1)班 | B. | 八(2)班 | C. | 八(3)班 | D. | 八(4)班 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
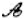 线”,点P为“
线”,点P为“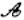 点”.
点”.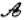 点”的坐标;
点”的坐标;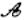 线”,并说明理由;
线”,并说明理由; 线”,求k的取值范围.
线”,求k的取值范围. 点”的⊙C的“
点”的⊙C的“ 线”,求r的值.
线”,求r的值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com