
某公司有甲种原料260kg,乙种原料270kg,计划用这两种原料生产A、B两种产品共40件.生产每件A种产品需甲种原料8kg,乙种原料5kg,可获利润900元;生产每件B种产品需甲种原料4kg,乙种原料9kg,可获利润1100元.设安排生产A种产品x件.
(1)完成下表
| 甲(kg) | 乙(kg) | 件数(件) |
A |
| 5x | x |
B | 4(40-x) |
| 40-x |
(2)安排生产A、B两种产品的件数有几种方案?试说明理由;
(3)设生产这批40件产品共可获利润y元,将y表示为x的函数,并求出最大利润.
(1)见解析
(2)共有三种方案:
方案一:A产品23件,B产品17件,
方案二:A产品24件,B产品16件,
方案三:A产品25件,B产品15件;
(3)y=-200x+44000 39400元
【解析】(1)根据总件数=单件需要的原料×件数列式即可;
(2)根据两种产品所需要的甲、乙两种原料列出不等式组,然后求解即可;
(3)根据总利润等于两种产品的利润之和列式整理,然后根据一次函数的增减性求出最大利润即可.
【解析】
(1)表格分别填入:A甲种原料8x,B乙种原料9(40-x);
(2)根据题意得,
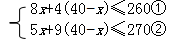
由①得,x≤25,
由②得,x≥22.5,
∴不等式组的解集是22.5≤x≤25,
∵x是正整数,
∴x=23、24、25,
共有三种方案:
方案一:A产品23件,B产品17件,
方案二:A产品24件,B产品16件,
方案三:A产品25件,B产品15件;
(3)y=900x+1100(40-x)=-200x+44000,
∵-200<0,
∴y随x的增大而减小,
∴x=23时,y有最大值,
y最大=-200×23+44000=39400元.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源:2014中考名师推荐数学分式(解析版) 题型:填空题
甲、乙两人两次同时在一家粮店购买大米,两次大米的价格分别为每千克a元和b元(a≠b).甲每次买100千克大米,乙每次买100元大米.
(1)用含a、b的代数式表示:甲两次购买大米共需付款 元,乙两次共购买 ___________千克大米.若甲两次购买大米的平均单价为每千克Q1元,乙两次购买大米的平均单价为每千克Q2元.则:Q1= ;Q2= .
(2)若规定谁两次购粮的平均价格低,谁购粮的方式就更合理,请你判断比较甲、乙两人的购粮方式,哪一个更合理,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学三角形(二)(解析版) 题型:填空题
在一张直角三角形纸片中,分别沿两直角边上一点与斜边中点的连线剪去两个三角形,得到如图所示的直角梯形,则原直角三角形纸片的斜边长是 ( )

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学三角形(一)(解析版) 题型:选择题
如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( )

A.25° B.30° C.45° D.60°
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学三角形(一)(解析版) 题型:选择题
一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )

A.90° B.100° C.130° D.180°
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学一次函数(解析版) 题型:选择题
一条直线y=kx+b,其中k+b=-5、kb=6,那么该直线经过( )
A.第二、四象限
B.第一、二、三象限
C.第一、三象限
D.第二、三、四象限
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学一元二次方程(解析版) 题型:解答题
阅读材料:设一元二次方程ax2+bx+c=0(a≠0)的两根为x1,x2,则两根与方程系数之间有如下关系:x1+x2=﹣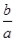 ,x1•x2=
,x1•x2=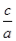 .
.
根据该材料填空:已知x1,x2是方程x2+6x+3=0的两实数根,则 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学一元一次不等式组(解析版) 题型:填空题
如图,用锤子以相同的力将铁钉垂直钉入木块,随着铁钉的深入,铁钉所受的阻力也越来越大.当铁钉未进入木块部分长度足够时,每次钉入木块的铁钉长度是前一次的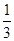 ,已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后,铁钉进入木块的长度是a cm,若铁钉总长度为6cm,则a的取值范围是 .
,已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后,铁钉进入木块的长度是a cm,若铁钉总长度为6cm,则a的取值范围是 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题(一)数学试卷(解析版) 题型:填空题
如图,□ABCD中,点E是AD边的中点,BE交对角线AC于点F,若AF=2,则对角线AC长为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com