
【题目】对于任意正实数a、b,因为![]() ≥0,所以a﹣
≥0,所以a﹣![]() ≥0,所以a+b≥
≥0,所以a+b≥![]() ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
【获得结论】在a+b≥2![]() (a、b均为正实数)中,若ab为定值p,则a+b≥2
(a、b均为正实数)中,若ab为定值p,则a+b≥2![]() ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2![]() .
.
根据上述内容,回答下列问题:若m>0,只有当m= 时,m+![]() 有最小值 .
有最小值 .
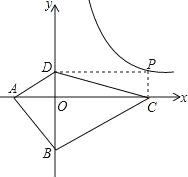
【探索应用】如图,已知A(﹣3,0),B(0,﹣4),P为双曲线![]() 上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
【答案】(1)1,2;(2)见试题解析。
【解析】
试题分析:(1)根据题目所给信息可知m+![]() ≥2
≥2![]() ,且当m=
,且当m=![]() 时等号成立,可得出答案;
时等号成立,可得出答案;
(2)可设P(x,![]() ),可表示出AC和BD,则四边形ABCD的面积为S四边形ABCD=2(x+
),可表示出AC和BD,则四边形ABCD的面积为S四边形ABCD=2(x+![]() )+12,再利用所给信息可得到其最小值,此时x=3,可得出AC=BD,可得出四边形ABCD为菱形.
)+12,再利用所给信息可得到其最小值,此时x=3,可得出AC=BD,可得出四边形ABCD为菱形.
试题解析:(1)根据题目所给信息可知m+![]() ≥2
≥2![]() ,且当m=
,且当m=![]() 时等号,
时等号,
∴当m=1时,m+![]() ≥2,即当m=1时,m+
≥2,即当m=1时,m+![]() 有最小值2,
有最小值2,
故答案为:1,2;
(2)设P(x,![]() ),则C(x,0),D(0,
),则C(x,0),D(0,![]() ),
),
∴CA=x+3,BD=![]() +4,
+4,
∴S四边形ABCD=![]() CA×BD=
CA×BD=![]() (x+3)(
(x+3)(![]() +4),
+4),
化简得:S=2(x+![]() )+12,∵x>0,
)+12,∵x>0,![]() >0,∴x+
>0,∴x+![]() ≥2
≥2![]() =6,
=6,
只有当x=![]() ,即x=3时,等号成立,∴S≥2×6+12=24.
,即x=3时,等号成立,∴S≥2×6+12=24.
∴S四边形ABCD有最小值24,此时,P(3,4),C(3,0),D(0,4),
AB=BC=CD=DA=5,∴四边形ABCD是菱形.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:初中数学 来源: 题型:
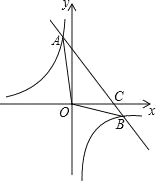
【题目】如图,已知一次函数y=ax+b的图象与反比例函数y=![]() 的图象相交于点A(﹣2,m)和点B(4,﹣2),与x轴交于点C
的图象相交于点A(﹣2,m)和点B(4,﹣2),与x轴交于点C
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店第一次用6000元购进了练习本若干本,第二次又用6000元购进该款练习本,但这次每本进货的价格是第一次进货价格的1.2倍,购进数量比第一次少了1000本.
(1)问:第一次每本的进货价是多少元?
(2)若要求这两次购进的练习本按同一价格全部销售完毕后获利不低于4500元,问每本售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
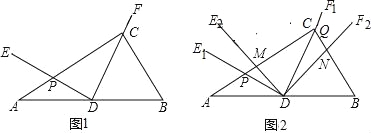
【题目】如图1,Rt△ABC中,∠ACB=90°,D为AB的中点,∠EDF=90°,DE交AC于点G,DF经过点C.
(1)若∠B=60°.
①求∠ADE的度数;
②如图2,将图1中的∠EDF绕点D顺时针方向旋转角α(0°<α<60°),旋转过程中的任意两个位置分别记为∠E1DF1,∠E2DF2,DE1交直线AC于点P,DF1交直线BC于点Q,DE2交直线AC于点M,DF2交直线BC于点N,求![]() 的值;
的值;
(2)将(1)问中的“若∠B=60°”改为“∠B=β(60°<β<90°)”,其余条件不变,判断![]() 的值是否为定值,如果是,请直接写出这个值(用含β的式子表示);如果不是,请说明理由.
的值是否为定值,如果是,请直接写出这个值(用含β的式子表示);如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店将某种商品按进货价提高100%后,又以6折优惠售出,售价为60元,则这种商品的进货价是( )
A. 120元 B. 100元 C. 72元 D. 50元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com