
【题目】如图1,Rt△ABC中,∠ACB=90°,D为AB的中点,∠EDF=90°,DE交AC于点G,DF经过点C.
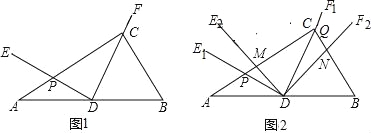
(1)若∠B=60°.
①求∠ADE的度数;
②如图2,将图1中的∠EDF绕点D顺时针方向旋转角α(0°<α<60°),旋转过程中的任意两个位置分别记为∠E1DF1,∠E2DF2,DE1交直线AC于点P,DF1交直线BC于点Q,DE2交直线AC于点M,DF2交直线BC于点N,求![]() 的值;
的值;
(2)将(1)问中的“若∠B=60°”改为“∠B=β(60°<β<90°)”,其余条件不变,判断![]() 的值是否为定值,如果是,请直接写出这个值(用含β的式子表示);如果不是,请说明理由.
的值是否为定值,如果是,请直接写出这个值(用含β的式子表示);如果不是,请说明理由.
【答案】(1)①∠ADE=30°;②![]() (2)见试题解析.
(2)见试题解析.
【解析】
试题分析:(1)根据含30°的直角三角形的性质和等边三角形的性质解答即可;
(2)根据相似三角形的判定和性质以及直角三角形中的三角函数解答即可;
(3)由(2)的推理得出![]() ,再利用直角三角形的三角函数解答.
,再利用直角三角形的三角函数解答.
试题解析:(1)①∵∠ACB=90°,D为AB的中点,∴CD=DB,∴∠DCB=∠B,
∵∠B=60°,∴∠DCB=∠B=∠CDB=60°,∴∠CDA=120°,∵∠EDC=90°,
∴∠ADE=30°;
②∵∠C=90°,∠MDN=90°,
∴∠DMC+∠CND=180°,
∵∠DMC+∠PMD=180°,
∴∠CND=∠PMD,
同理∠CPD=∠DQN,
∴△PMD∽△QND,
过点D分别做DG⊥AC于G,DH⊥BC于H,
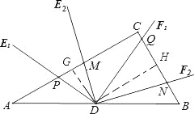
可知DG,DH分别为△PMD和△QND的高,∴![]() =
=![]() ,∵DG⊥AC于G,DH⊥BC于H,∴DG∥BC,又∵D为AC中点,∴G为AC中点,∵∠C=90°,∴四边形CGDH 为矩形有CG=DH=AG,
,∵DG⊥AC于G,DH⊥BC于H,∴DG∥BC,又∵D为AC中点,∴G为AC中点,∵∠C=90°,∴四边形CGDH 为矩形有CG=DH=AG,
Rt△AGD中,![]() =
=![]() ,即
,即![]() =
=![]() .
.
(2)是定值,定值为tan(90°﹣β),∵![]() =
=![]() ,四边形CGDH 为矩形有CG=DH=AG,
,四边形CGDH 为矩形有CG=DH=AG,
∴Rt△AGD中, ![]() =tan∠A=tan(90°﹣∠B)=tan(90°﹣β),∴
=tan∠A=tan(90°﹣∠B)=tan(90°﹣β),∴![]() =tan(90°﹣β).
=tan(90°﹣β).


科目:初中数学 来源: 题型:
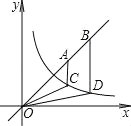
【题目】双曲线y=![]() (x>0)与直线y=x在坐标系中的图象如图所示,点A、B在直线上AC、BD分别平行y轴,交曲线于C、D两点,若BD=2AC,则4OC2﹣OD2的值为 .
(x>0)与直线y=x在坐标系中的图象如图所示,点A、B在直线上AC、BD分别平行y轴,交曲线于C、D两点,若BD=2AC,则4OC2﹣OD2的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小雨写了几个多项式,其中是五次三项式的是( )
A. y5-1 B. 5x2y2-x+y C. 3a2b2c-ab+1 D. 3a5b-b+c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 三点确定一个圆 B. 经过圆心的直线是圆的对称轴
C. 一条弦所对的圆周角等于圆心角的一半 D. 三角形的外心到三角形三边距离相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意正实数a、b,因为![]() ≥0,所以a﹣
≥0,所以a﹣![]() ≥0,所以a+b≥
≥0,所以a+b≥![]() ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
【获得结论】在a+b≥2![]() (a、b均为正实数)中,若ab为定值p,则a+b≥2
(a、b均为正实数)中,若ab为定值p,则a+b≥2![]() ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2![]() .
.
根据上述内容,回答下列问题:若m>0,只有当m= 时,m+![]() 有最小值 .
有最小值 .
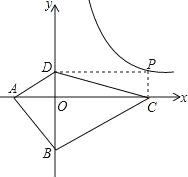
【探索应用】如图,已知A(﹣3,0),B(0,﹣4),P为双曲线![]() 上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式从左到右的变形是因式分解的是( )
A.x2+2x+3=(x+1)2+2
B.(x+y)(x﹣y)=x2﹣y2
C.x2﹣xy+y2=(x﹣y)2
D.2x﹣2y=2(x﹣y)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com