
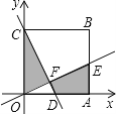
【题目】如图,在直角坐标系中,正方形OABC顶点B的坐标为(6,6),直线CD交直线OA于点D,直线OE交线段AB于点E,且CD⊥OE,垂足为点F,若图中阴影部分的面积是正方形OABC的面积的![]() ,则△OFC的周长为______.
,则△OFC的周长为______.
【答案】6+2![]()
【解析】
证明△COD≌△OAE,推理出△OCF面积=四边形FDAE面积=12÷2=6,设OF=x,FC=y,则xy=12,x2+y2=36,所以(x+y)2=x2+y2+2xy=60,从而可得x+y的值,则△OFC周长可求.
∵正方形OABC顶点B的坐标为(6,6),
∴正方形的面积为36.
所以阴影部分面积为36×![]() =12.
=12.
∵四边形AOCB是正方形,
∴∠AOC=90°,即∠COE+∠AOE=90°,
又∵CD⊥OE,
∴∠CFO=90°
∴∠OCF+∠COF=90°,
∴∠OCD=∠AOE
在△COD和△OAE中

∴△COD≌△OAE(AAS).
∴△COD面积=△OAE面积.
∴△OCF面积=四边形FDAE面积=12÷2=6.
设OF=x,FC=y,
则xy=12,x2+y2=36,
所以(x+y)2=x2+y2+2xy=60.
所以x+y=2![]() .
.
所以△OFC的周长为6+2![]() .
.
故答案为6+2![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
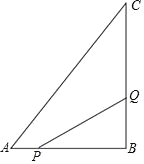
【题目】在△ABC中,AB=10cm,BC=16cm,∠B=90°,点P从点A开始沿着AB边向点B以1cm/s的速度移动(到B停止),点Q从点B开始沿着BC边向点C以2cm/s的速度移动(到C停止).如果P、Q分别从A、B同时出发,经过几秒钟,使△PBQ的面积是△ABC面积的![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
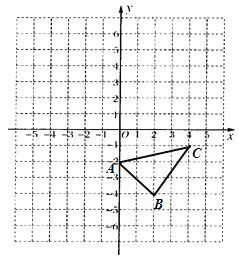
【题目】已知:如图,在平面直角坐标系中.
(1)作出△ABC关于![]() 轴对称的
轴对称的![]() ,并写出
,并写出![]() 三个顶点的坐标:
三个顶点的坐标: ![]() ( ),
( ),![]() ( ),
( ),![]() ( );
( );
(2)直接写出△ABC的面积为 ;
(3)在![]() 轴上画点P,使PA+PC最小.
轴上画点P,使PA+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
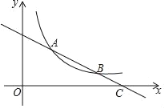
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象相交于A(2,3)、B(a,1)两点.
(x>0)的图象相交于A(2,3)、B(a,1)两点.
(1)求这两个函数的表达式;
(2)求证:AB=2BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图(1)、(2)所示的△ABC中,AB=4,AC=6.将△ABC沿图示中的虚线剪开裁剪办法已在图上标注,对于各图中剪下的两个阴影三角形而言,下列说法正确的是( )
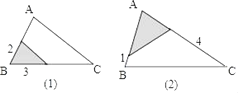
A. 只有(1)中的与△ABC相似 B. 只有(2)中的与△ABC相似
C. 都与△ABC相似 D. 都与△ABC不相似
查看答案和解析>>
科目:初中数学 来源: 题型:
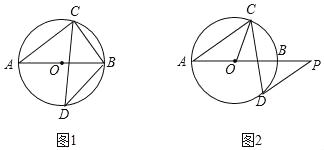
【题目】已知AB是⊙O的直径,弦CD与AB相交,∠BAC=40°.
(1)如图1,若D为弧AB的中点,求∠ABC和∠ABD的度数;
(2)如图2,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
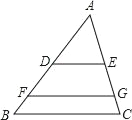
【题目】如图,在△ABC中,点D,F在AB上,点E,G在AC上,DE∥FG∥BC,且S△ADE=S四边形DFGE=S四边形FBCG
(1)求DE:FG:BC的值;
(2)若AB=10,AC=15,BC=12,求四边形DFGE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“作已知三角形的高”的尺规作图过程.
已知: ![]() .
.

求作: ![]() 边上的高
边上的高![]()
作法:如图,
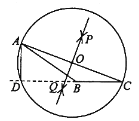
(1)分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧相交于
的长为半径作弧,两弧相交于![]() ,
, ![]() 两点;
两点;
(2)作直线![]() ,交
,交![]() 于点
于点![]() ;
;
(3)以![]() 为圆心,
为圆心, ![]() 为半径⊙O,与CB的延长线交于点D,连接AD,线段AD即为所作的高.
为半径⊙O,与CB的延长线交于点D,连接AD,线段AD即为所作的高.
请回答;该尺规作图的依据是___________________________________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
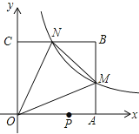
【题目】如图,在平面直角坐标系中,反比例函数![]() 的图象与边长是6的正方形OABC的两边AB、BC分别相交于M、N两点,△OMA的面积为6.
的图象与边长是6的正方形OABC的两边AB、BC分别相交于M、N两点,△OMA的面积为6.
(1)求反比例函数![]() 的解析式;
的解析式;
(2)若动点P在x轴上,求PM+PN的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com