
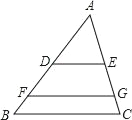
【题目】如图,在△ABC中,点D,F在AB上,点E,G在AC上,DE∥FG∥BC,且S△ADE=S四边形DFGE=S四边形FBCG
(1)求DE:FG:BC的值;
(2)若AB=10,AC=15,BC=12,求四边形DFGE的周长.
【答案】(1)1:![]() :
:![]() (2)
(2)![]()
【解析】
(1)由DE∥FG∥BC知△ADE∽△AFG∽△ABC,根据题意可得![]() ,
,![]() ,利用相似三角形的性质即可得出答案;
,利用相似三角形的性质即可得出答案;
(2)由![]() 、BC=12知FG=4
、BC=12知FG=4![]() ,由
,由![]() 、FG=4
、FG=4![]() 知DE=4
知DE=4![]() ,从而得DF=
,从而得DF=![]() ,同理求得GE=5
,同理求得GE=5![]() -5
-5![]() ,根据周长公式即可得出答案.
,根据周长公式即可得出答案.
(1)∵S△ADE=S梯形DFGE=S梯形FBCG,
∵DE∥FG∥BC,
∴△ADE∽△AFG∽△ABC,
∴![]() ,
,![]() ,
,
由于相似三角形的面积比等于对应边长的平方比,
∴DE:FG:BC=1:![]() .
.
(2)∵![]() ,BC=12,
,BC=12,
∴FG=![]() ,
,
∵![]() ,FG=4
,FG=4![]() ,
,
∴DE=![]() ,
,
∴DF=![]() ,
,
同理可得GE=5![]() ﹣5
﹣5![]() ,
,
∴四边形DFGE的周长为DF+FG+GE+DE
=![]() +4
+4![]() +5
+5![]() ﹣5
﹣5![]() +4
+4![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
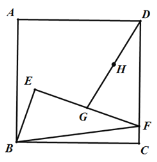
【题目】如图,E为正方形ABCD内一点,点F在CD边上,且∠BEF=90°,EF=2BE.点G为EF的中点,点H为DG的中点,连接EH并延长到点P,使得PH=EH,连接DP.
(1)依题意补全图形;
(2)求证:DP=BE;
(3)连接EC,CP,猜想线段EC和CP的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
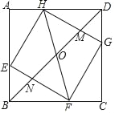
【题目】在边长为3的正方形ABCD中,点E、F、G、H分别在AB、BC、CD、DA边上,且满足EB=FC=GD=HA=1,BD分别与HG、HF、EF相交于M、O、N给出以下结论:
①HO=OF;②OF2=ONOB;③HM=2MG;④S△HOM=![]() ,其中正确的个数有( )
,其中正确的个数有( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
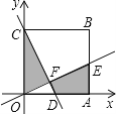
【题目】如图,在直角坐标系中,正方形OABC顶点B的坐标为(6,6),直线CD交直线OA于点D,直线OE交线段AB于点E,且CD⊥OE,垂足为点F,若图中阴影部分的面积是正方形OABC的面积的![]() ,则△OFC的周长为______.
,则△OFC的周长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意三个实数a,b,c,用min|a,b,c|表示这三个实数中最小数,例如:min|-2,0,1|=-2,则:
(1)填空,min|(-2019)0,(-![]() )-2,-
)-2,-![]() |=______,如果min|3,5-x,3x+6|=3,则x的取值范围为______;
|=______,如果min|3,5-x,3x+6|=3,则x的取值范围为______;
(2)化简:![]() ÷(x+2+
÷(x+2+![]() )并在(1)中x的取值范围内选取一个合适的整数代入求值.
)并在(1)中x的取值范围内选取一个合适的整数代入求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
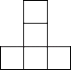
【题目】用若干个小立方块搭成一个几何体,使它从正面看与从左面看都是如图的同一个图.通过实际操作,并与同学们讨论,解决下列问题:
(1)所需要的小立方块的个数是多少?你能找出几种?
(2)画出所需个数最少和所需个数最多的几何体从上面看到的图,并在小正方形里注明在该位置上小立方块的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
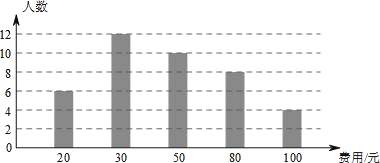
【题目】在全民读书月活动中,某校随机抽样调查了一部分学生本学期计划购买课外书的费用情况,根据图中的相关信息,解答下面问题;
(1)这次调查获取的样本容量是 ;
(2)由统计图可知,这次调查获取的样本数据的众数是 ;中位数是 ;
(3)求这次调查获取的样本数据的平均数;
(4)若该校共有1000名学生,根据样本数据,估计该校本学期计划购买课外书的总花费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式,能够表示图中阴影部分的面积的是( )
①ac+(b﹣c)c;②ac+bc﹣c2;③ab﹣(a﹣c)(b﹣c);④(a﹣c)c+(b﹣c)c+c2

A. ①②③④ B. ①②③ C. ①② D. ①
查看答案和解析>>
科目:初中数学 来源: 题型:
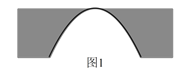
【题目】河上有一座桥孔为抛物线形的拱桥(如图 ![]() ),水面宽
),水面宽 ![]() 时,水面离桥孔顶部
时,水面离桥孔顶部 ![]() ,因降暴雨水面上升
,因降暴雨水面上升 ![]() .
.
(1)建立适当的坐标系,并求暴雨后水面的宽;(结果保留根号)
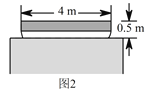
(2)一艘装满物资的小船,露出水面的部分高为 ![]() ,宽
,宽 ![]() (横断面如图
(横断面如图 ![]() 所示),暴雨后这艘船能从这座拱桥下通过吗?
所示),暴雨后这艘船能从这座拱桥下通过吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com