
����Ŀ������ע�س����̻�������������������½������ƻ�����ס����������繲800�꣬��������ÿ��12Ԫ����������ÿ��15Ԫ��������ϱ������ס�����������ijɻ��ʷֱ�Ϊ85%��90%��
��1�����������������繲��ȥ10500Ԫ����ס��������������������ꣿ
��2����Ҫʹ����������ܳɻ��ʲ�����88%��������������������ꣿ
��3���ڣ�2���������£�Ӧ���ѡ�����磬ʹ��������ķ�����ͣ��������ͷ��ã�
���𰸡���1�������������500�꣬��������300�ꣻ
��2���������������320�ꣻ
��3�������������320�꣬��������480�꣬����������������ijɻ��ʲ�����88%����ʹ��������ķ�����ͣ�����ͷ���Ϊ11040Ԫ��
�������������������1�����ݹؼ�������������ס����������繲800�꣬�����������������繲��21000Ԫ�����г���������⣮
��2�����ҵ��ؼ�����������������ijɻ��ʲ�����88%���������ҵ���������ĵ�����ϵ���г�����ʽ������������ȡֵ��Χ��
��3���ٸ��������г�������������ķ���֮�����������ĺ�����ϵʽ������һ�κ��������������ͷ��ã�
�����������1���蹺���������x�꣬����������y�꣬������ã�
![]()
���![]()
�𣺹����������500�꣬��������300�꣮
��2����������繺��z�꣬������ã�
85%z+90%��800-z����800��88%��
���z��320��
�𣺼������������320�꣮
��3���蹺����������ķ���֮��Ϊm����
m=12z+15��800-z��=12000��3z��
�ڴ˺����У�m��z���������С
���Ե�z=320ʱ��mȡ����Сֵ������СֵΪ12000��3��320=11040Ԫ
�𣺹����������320�꣬��������480�꣬����������������ijɻ��ʲ�����88%����ʹ��������ķ�����ͣ�����ͷ���Ϊ11040Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(8��)��ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y��kx��b��ͼ���뷴��������y��![]() ��ͼ����A(2��3)��B(��3��n)���㣮
��ͼ����A(2��3)��B(��3��n)���㣮
(1)��һ�κ����ͷ����������Ľ���ʽ��
(2)��P��y����һ�㣬��������PAB�������5����OP�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��ʵ�ĵ��ԭ�������������·����0��0������0��1������1��0������1��1������1��2������ÿ���˶�һ���㣬���˶�����2017��ʱʵ�ĵ�����λ�õĺ�����Ϊ�� �� 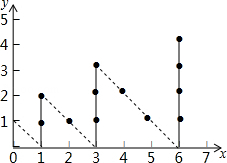
A.45
B.946
C.990
D.1035
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߶�AB �� AD���ڵ�A �� CΪֱ��AD��һ�㣨�����A �� D�غϣ�������C��BC���Ҳ�������CE��BC �� ����D��ֱ��DF��AB �� ��CE�ڵ�G��G��D���غϣ���
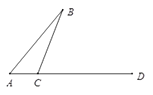
��1����ͼ1������C���߶�AD�ϣ��ҡ�BCAΪ�۽ǣ��ٰ�Ҫ��ȫͼ�Σ����жϡ�B���CGD��������ϵ����֤����
��2������C���߶�DA���ӳ����ϣ���ֱ��д����B���CGD��������ϵ��
��3�������ϱ�����������һ���µ���չ���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������������ǣ� ��
A. �Խ�����ȵ��ı����Ǿ���
B. �Խ����ഹֱ���ı����Ǿ���
C. �Խ����ഹֱ�ľ�����������
D. �ı���ȵ�ƽ���ı�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A. �����ε���ͶӰһ����������B. ���������ͶӰһ���dz�����
C. �����ͶӰһ����ԲD. Բ����ͶӰһ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ� ��
A.aa3=a3
B.��ab��3=a3b
C.��a3��2=a6
D.a8��a4=a2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com