
【题目】如图,平面直角坐标系中,![]() ,
,![]() 为
为![]() 轴正半轴上一点,连接
轴正半轴上一点,连接![]() ,在第一象限作
,在第一象限作![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() 轴于
轴于![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,且
,且![]() ,则直线
,则直线![]() 解析式为____________.
解析式为____________.

【答案】![]()
【解析】
过A作AM⊥y轴,交y轴于M,交CD于N,根据∠BMA=∠ANC=90°,∠BAC=90°可以得到∠ABM=∠CAN,再根据A点坐标可以得出OM=DN=AM=4,求出△ABM≌△CAN,根据全等的性质求出AN=BM,CN=4,再根据ED=5EC和E在直线y=x上求出E的坐标,即可求出MN=10,CD=8,AN=BM=MN-AM=6的值,得出C(10,8),B(0,10)代入y=kx+b中,即可求出.
解:过![]() 作
作![]() 轴,交
轴,交![]() 轴于
轴于![]() ,交
,交![]() 于
于![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
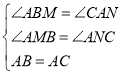 ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 设
设![]() ,
,![]() ,
,
![]() ,
,
![]() 点
点![]() 在直线
在直线![]() 上,
上,
![]() ,
,
则![]() ,
,
![]() ,即
,即![]() ,
,![]() .
.
![]() 点
点![]() 在直线
在直线![]() 上,
上,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
设直线![]() 的解析式是
的解析式是![]() ,
,
把![]() 代入得:
代入得:![]() ,
,
即直线![]() 的解析式是
的解析式是![]() ,
,
故答案为:![]() .
.



 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)求共抽取了多少名学生的征文;
(2)将上面的条形统计图补充完整;
(3)在扇形统计图中,选择“爱国”主题所对应的圆心角是多少;
(4)如果该校九年级共有1200名学生,请估计选择以“友善”为主题的九年级学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出①,②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分)与费用y(元)之间的函数关系如图所示.
(1)有月租的收费方式是________(填“①”或“②”),月租费是________元;
(2)分别求出①,②两种收费方式中y与自变量x之间的函数表达式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
(1)求证:四边形AGBD为平行四边形;
(2)若四边形AGBD是矩形,则四边形BEDF是什么特殊四边形?证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织一项公益知识竞赛,比赛规定:每个班级由2名男生、2名女生及1名班主任老师组成代表队.但参赛时,每班只能有3名队员上场参赛,班主任老师必须参加,另外2名队员分别在2名男生和2名女生中各随机抽出1名.初三(1)班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队,求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率.(请用“画树状图”或“列表”或“列举”等方法给出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为

A. 4 B. ![]() C. 6 D.
C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D、E分别在BC、AC上,且CD=AE,AD与BE相交于P,BQ⊥AD于Q.
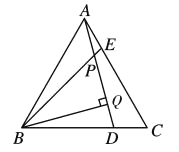
(1)求证:![]() ;
;
(2)若PQ=4,PE=1,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知AB⊥BD,ED⊥BD,AB=CD,BC=DE
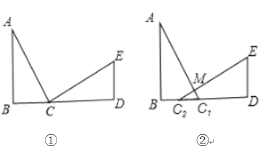
(1)求证:△ABC≌△CDE
(2)试判断AC与CE的位置关系,并说明理由.
(3)若将CD沿CB方向平移得到图②的情形,其余条件不变,此时第(2)问中AC与CE的位置关系还成立吗?请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com