
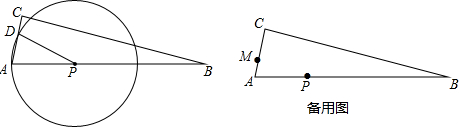
分析 (1)过点P作PH⊥AC,垂足为H,如图1,利用三角函数可得AH=$\frac{1}{4}$x,根据勾股定理可得PH=$\frac{\sqrt{15}}{4}$x,根据垂径定理可得AD=2AH=$\frac{1}{2}$x,从而可得CD=4-$\frac{1}{2}$x,即可得到y与x的关系;
(2)过点P作PG⊥BC,垂足为G,如图2,根据同圆中相等的弦所对的弦心距相等可得PH=PG=$\frac{\sqrt{15}}{4}$x,在Rt△PGB中,运用三角函数即可求出AP的值;
(3)设⊙P与⊙C的公共弦EF与PC交于点O,如图3,根据勾股定理可得CO=$\frac{\sqrt{2}}{2}$,P0=$\sqrt{{x}^{2}-\frac{1}{2}}$,从而有CP=$\sqrt{{x}^{2}-\frac{1}{2}}$+$\frac{\sqrt{2}}{2}$,然后在Rt△CHP中,运用勾股定理即可求出x的值.
解答 解:(1)过点P作PH⊥AC,垂足为H,连接PC,如图1,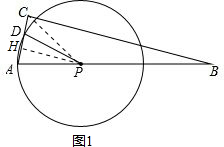
则有AH=APcosA=$\frac{1}{4}$x,PH=$\sqrt{A{P}^{2}-A{H}^{2}}$=$\frac{\sqrt{15}}{4}$x,
AD=2AH=$\frac{1}{2}$x,CD=AC-AD=4-$\frac{1}{2}$x,
∴y=$\frac{1}{2}$CD•PH=$\frac{1}{2}$×(4-$\frac{1}{2}$x)×$\frac{\sqrt{15}}{4}$x=-$\frac{\sqrt{15}}{16}$x2+$\frac{\sqrt{15}}{2}$x(0<x<8);
(2)过点P作PG⊥BC,垂足为G,如图2,
∵⊙P被直线BC和直线AC截得的弦长相等,
∴PH=PG=$\frac{\sqrt{15}}{4}$x.
在Rt△ACB中,AC=AB•cosA,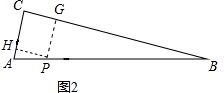
∴4=$\frac{1}{4}$AB,即AB=16,
∴BP=AB-AP=16-x.
在Rt△PGB中,
∵sinB=$\frac{PG}{BP}$,sinB=cosA=$\frac{1}{4}$,PG=$\frac{\sqrt{15}}{4}$x,BP=16-x,
∴$\frac{\sqrt{15}}{4}$x=$\frac{1}{4}$(16-x),
解得:x=$\frac{8\sqrt{15}-8}{7}$,
∴AP=$\frac{8\sqrt{15}-8}{7}$;
(3)设⊙P与⊙C的公共弦EF与PC交于点O,如图3,
则有EF=$\sqrt{2}$,EO=OF=$\frac{1}{2}$EF=$\frac{\sqrt{2}}{2}$,PC⊥EF,CE=CF=1,PE=PF=x,
∴CO=$\sqrt{C{E}^{2}-O{E}^{2}}$=$\frac{\sqrt{2}}{2}$,P0=$\sqrt{P{E}^{2}-O{E}^{2}}$=$\sqrt{{x}^{2}-\frac{1}{2}}$,
∴CP=OP+CO=$\sqrt{{x}^{2}-\frac{1}{2}}$+$\frac{\sqrt{2}}{2}$.
在Rt△CHP中,
∵CH2+PH2=PC2,
∴(4-$\frac{1}{4}$x)2+($\frac{\sqrt{15}}{4}$x)2=($\sqrt{{x}^{2}-\frac{1}{2}}$+$\frac{\sqrt{2}}{2}$)2,
整理得16-2x=$\sqrt{2{x}^{2}-1}$,
∴(16-2x)2=2x2-1,
整理得2x2-64x+257=0,
解得:x1=$\frac{32-\sqrt{510}}{2}$,x2=$\frac{32+\sqrt{510}}{2}$.
∵点P是边AB上的动点,
∴AP=x≤16,
∴AP=$\frac{32-\sqrt{510}}{2}$.
点评 本题主要考查了垂径定理、相交两圆的性质、勾股定理、三角函数、同圆或同圆中弦与弦心距之间的关系等知识,要求一个未知数的值,通常可运用相似三角形的性质、勾股定理或三角函数建立方程,然后解这个方程就可解决问题.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
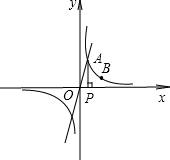 已知正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为P点,已知△OAP的面积为1.
已知正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为P点,已知△OAP的面积为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
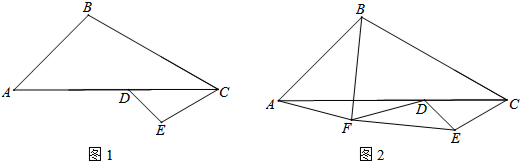
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
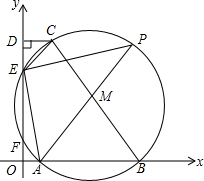 在平面直角坐标系中,以BC为直径的⊙M交x轴正半轴于点A、B,交y轴正半轴于点E、F,作CD⊥y轴于D连接AM并延长交⊙M于点P,连接PE、AF.
在平面直角坐标系中,以BC为直径的⊙M交x轴正半轴于点A、B,交y轴正半轴于点E、F,作CD⊥y轴于D连接AM并延长交⊙M于点P,连接PE、AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com