
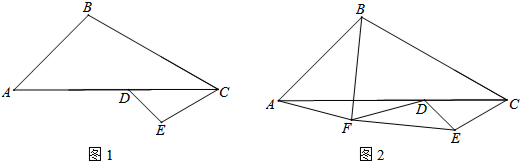
分析 (1)过点E作EN⊥DC于点N,证明△ABC∽△DEC.得出对应边成比例$\frac{DE}{AB}=\frac{DC}{AC}$,求DE,再在△DEC中,由∠EDC=45°,∠DCE=30°,求出DN=EN=$\sqrt{2}$,即可得出CE=2EN=$\sqrt{2}$DE=2$\sqrt{2}$;
(2)①过点F作FM⊥FD交AB于点M,连接MD,先证明△AMF为等边三角形,得出FM=AF=FD=AM,得出∠FMD=∠FDM=45°,再证出MD∥BC,得出比例式求出MB=DE,即可得出结论;
②由三角形的面积公式=$\frac{1}{2}$absinC,分别求出五边形ABCEF的面积、△ABF的面积、△BCE的面积,△BEF的面积=五边形ABCEF的面积-△ABF的面积-△BCE的面积,即可得出结果.
解答 解:(1)过点E作EN⊥DC于点N,如图1所示: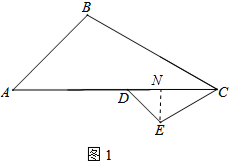
在△ABC和△DEC中,
∵∠A=∠EDC,∠ACB=∠DCE,
∴△ABC∽△DEC.
∴$\frac{DE}{AB}=\frac{DC}{AC}$,
∵AB=5,$\frac{DC}{AC}$=25,
∴DE=2.
在△DEC中,∠EDC=45°,∠DCE=30°,
∴DN=EN=$\sqrt{2}$,CE=2EN=$\sqrt{2}$DE,CN=$\sqrt{3}$EN=$\sqrt{6}$,
∴CE=2$\sqrt{2}$.
(2)①证明:过点F作FM⊥FD交AB于点M,连接MD,如图2所示: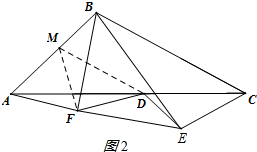
∵∠FAD=∠FDA=15°,
∴AF=DF,∠AFD=150°.
∴∠AFM=60°.
∵∠MAF=∠BAC+∠DAF=60°,
∴△AMF为等边三角形.
∴FM=AF=FD=AM,
∴∠FMD=∠FDM=45°.
∴∠AMD=105°=∠ABC.
∴MD∥BC,
∴$\frac{MB}{DC}=\frac{AB}{AC}$.
由(1)知:$\frac{DE}{DC}=\frac{AB}{AC}$,
∴$\frac{MB}{DC}=\frac{DE}{DC}$,
∴MB=DE.
∴AB=DF+DE.
②由①得:DF=AB-DE=3,
∴FM=FD=AM=3,
∴MD=3$\sqrt{2}$,
∵MD∥BC,
∴MD:BC=AM:AB,
即3$\sqrt{2}$:BC=3:5,
∴BC=5$\sqrt{2}$,
∵DC:AC=2:5,CD=$\sqrt{2}$+$\sqrt{6}$,
∴AC=$\frac{5(\sqrt{2}+\sqrt{6})}{2}$,
∵△ABC的面积=$\frac{1}{2}$×AB×ACsin45°=$\frac{1}{2}$×5×$\frac{5(\sqrt{2}+\sqrt{6})}{2}$×$\frac{\sqrt{2}}{2}$=$\frac{25+25\sqrt{3}}{4}$,
△ADF的面积=$\frac{1}{2}$×AF×DFsin150°=$\frac{1}{2}$×3×3×$\frac{1}{2}$=$\frac{9}{4}$,
△CDE的面积=$\frac{1}{2}$×CD×CEsin30°=$\frac{1}{2}$×($\sqrt{2}$+$\sqrt{6}$)×2$\sqrt{2}$×$\frac{1}{2}$=1+$\sqrt{3}$,
△DEF的面积=$\frac{1}{2}$×DE×DFsin120°=$\frac{1}{2}$×2×3×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$,
△ABF的面积=$\frac{1}{2}$×AB×AFsin60°=$\frac{1}{2}$×5×3×$\frac{\sqrt{3}}{2}$=$\frac{15\sqrt{3}}{4}$,
△BCE的面积=$\frac{1}{2}$×BC×CEsin60°=$\frac{1}{2}$×5$\sqrt{2}$×2$\sqrt{2}$×$\frac{\sqrt{3}}{2}$=5$\sqrt{3}$,
∴△BEF的面积=五边形ABCEF的面积-△ABF的面积-△BCE的面积=($\frac{25+25\sqrt{3}}{4}$+$\frac{9}{4}$+1+$\sqrt{3}$+$\frac{3\sqrt{3}}{2}$)-$\frac{15\sqrt{3}}{4}$-5$\sqrt{3}$=$\frac{19}{2}$.
点评 本题是相似形综合题,考查了相似三角形的判定与性质、等腰直角三角形的性质、等边三角形的判定与性质、平行线的判定与性质、三角函数的运用以及三角形面积的计算方法等知识;本题难度较大,综合性强,特别是(2)中,需要通过作辅助线证明平行线以及间接计算三角形的面积才能得出结果.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | 4cm | B. | $4\sqrt{2}$cm | C. | $4\sqrt{3}$cm | D. | 6cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
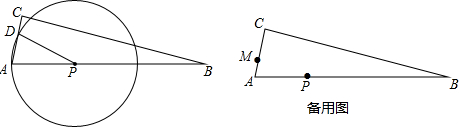
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
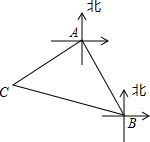 如图,已知小岛B在基地A的南偏东30°方向上,与基地A相距10海里,货轮C在基地A的南偏西60°方向、小岛B的北偏西75°方向上,那么货轮C与小岛B的距离是10$\sqrt{2}$海里.
如图,已知小岛B在基地A的南偏东30°方向上,与基地A相距10海里,货轮C在基地A的南偏西60°方向、小岛B的北偏西75°方向上,那么货轮C与小岛B的距离是10$\sqrt{2}$海里.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 下降高度d(米) | 20 | 80 | 245 | 320 |
| 下降时间t(秒) | 2 | 4 | 7 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com