
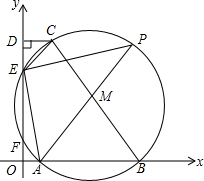
 在平面直角坐标系中,以BC为直径的⊙M交x轴正半轴于点A、B,交y轴正半轴于点E、F,作CD⊥y轴于D连接AM并延长交⊙M于点P,连接PE、AF.
在平面直角坐标系中,以BC为直径的⊙M交x轴正半轴于点A、B,交y轴正半轴于点E、F,作CD⊥y轴于D连接AM并延长交⊙M于点P,连接PE、AF.分析 (1)根据四边形APEF是⊙M的内接四边形的性质可知∠APE=∠AFO,利用EAM=90°-∠APE,∠FAO=90°-∠AFO得到∠FAO=∠EAM;
(2)利用顶点公式可知C点的坐标($\frac{b}{2}$,$\frac{{b}^{2}+4c}{4}$),图象过E点,得E点的坐标为(0,c),连接AC,OC,则AC⊥OB,CD⊥y轴,AO⊥OD,可证明四边形OACD为矩形,得到DC=OA,S四边形OECB=S△OCE+S△OCB=$\frac{1}{2}$OE•CD+$\frac{1}{2}$OB•AC=$\frac{1}{2}$(c•$\frac{b}{2}$+2×$\frac{{b}^{2}+4c}{4}$)=$\frac{{b}^{2}+4c+bc}{4}$=$\frac{11}{4}$,所以b2+4c+bc=11,把点B(2,0)代入可得-4+2b+c=0,联立方程组解得b=1,c=2,所以过B、C、E三点的二次函数的解析式为y=-x2+x+2.
解答 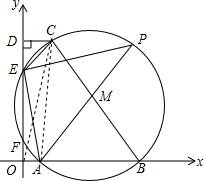 (1)证明:∵四边形APEF是圆M的内接四边形,
(1)证明:∵四边形APEF是圆M的内接四边形,
∴∠P=∠AFO,
∵AP是⊙M的直径,
∴∠AEP=∠AOF=90°,
∴∠FAO+∠AFO=∠EAM+∠P=90°,
∴∠FAO=∠EAM;
(2)解:连接AC、OC,
由抛物线y=-x2+bx+c可知顶点C($\frac{b}{2}$,$\frac{{b}^{2}+4c}{4}$),E(0,c),
∵BC是⊙M的直径,
∴∠BAC=90°,
∴AC⊥OB,
∴AC=$\frac{{b}^{2}+4c}{4}$,
∵CD⊥y轴,AO⊥OD,
∴四边形OACD为矩形
∴DC=$\frac{b}{2}$,
∴S四边形OECB=S△OCE+S△OCB=$\frac{1}{2}$OE•CD+$\frac{1}{2}$OB•AC=$\frac{1}{2}$(c•$\frac{b}{2}$+2×$\frac{{b}^{2}+4c}{4}$)=$\frac{{b}^{2}+4c+bc}{4}$=$\frac{11}{4}$,
∴b2+4c+bc=11,
∵抛物线y=-x2+bx+c经过点B(2,0),
∴-4+2b+c=0,
∴解$\left\{\begin{array}{l}{{b}^{2}+4c+bc=11}\\{-4+2b+c=0}\end{array}\right.$得$\left\{\begin{array}{l}{b=1}\\{c=2}\end{array}\right.$或$\left\{\begin{array}{l}{b=-5}\\{c=14}\end{array}\right.$(不合题意,舍去),
∴过点B、C、E,且以C为顶点的抛物线为y═-x2+x+2.
点评 本题考查二次函数的综合应用,其中涉及到的知识点圆内接四边形的性质,二次函数顶点坐标求法以及函数的交点的意义等,要熟练掌握才能灵活运用.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:解答题
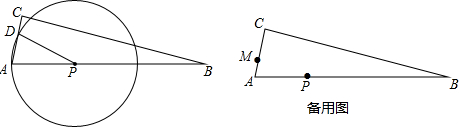
 如图,在矩形ABCD中,AB=2$\sqrt{3}$,BC=6,将该矩形沿对角线BD翻折,C的对应点为G,使△DBG与△DBC在同一平面内,BG交AD于点E,在DA延长线上取点F,使AE=AF,连接BF.
如图,在矩形ABCD中,AB=2$\sqrt{3}$,BC=6,将该矩形沿对角线BD翻折,C的对应点为G,使△DBG与△DBC在同一平面内,BG交AD于点E,在DA延长线上取点F,使AE=AF,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
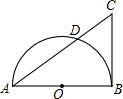 如图,AB是半圆O的直径,CB是半圆O的切线,B是切点,AC交半圆O于点D,已知CD=1,AD=4,则tan∠CAB=$\frac{1}{2}$.
如图,AB是半圆O的直径,CB是半圆O的切线,B是切点,AC交半圆O于点D,已知CD=1,AD=4,则tan∠CAB=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
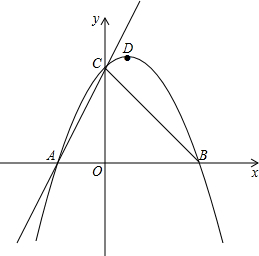 如图,在平面直角坐标系中,拋物线y=-$\frac{1}{2}$x2+bx+4与直线y=kx+4交于点A、C,与x轴交于点A、B,点A在原点左侧,点D是该拋物线的顶点.已知tan∠OCA=$\frac{1}{2}$,连接CB.
如图,在平面直角坐标系中,拋物线y=-$\frac{1}{2}$x2+bx+4与直线y=kx+4交于点A、C,与x轴交于点A、B,点A在原点左侧,点D是该拋物线的顶点.已知tan∠OCA=$\frac{1}{2}$,连接CB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com