
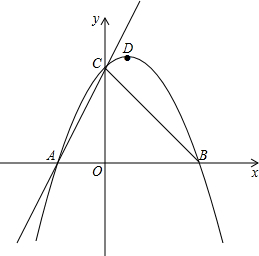
 ��ͼ����ƽ��ֱ������ϵ�У�������y=-$\frac{1}{2}$x2+bx+4��ֱ��y=kx+4���ڵ�A��C����x�ύ�ڵ�A��B����A��ԭ����࣬��D�ǸÒ����ߵĶ��㣮��֪tan��OCA=$\frac{1}{2}$������CB��
��ͼ����ƽ��ֱ������ϵ�У�������y=-$\frac{1}{2}$x2+bx+4��ֱ��y=kx+4���ڵ�A��C����x�ύ�ڵ�A��B����A��ԭ����࣬��D�ǸÒ����ߵĶ��㣮��֪tan��OCA=$\frac{1}{2}$������CB������ ��1�������C�����꣬������֪�ó�A��-2��0��������y=-$\frac{1}{2}$x2+bx+4���b=1��Ȼ����y=0����0=-$\frac{1}{2}$x2+x+4���ⷽ�̼������B�����꣬�������AB=6��Ȼ����������������ʽ��ü��ɣ�
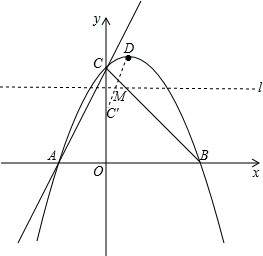
��2�����������ߵĽ���ʽ�ɵó�����D�����꣬��ֱ��y=3��Ȼ������C����ֱ��y=3�ĶԳƵ�C�䣬����C��D����ֱ��y=3��M��M��Ϊ����MC+MD����Сֵ����C��D�ij�����ֱ��C��D�Ľ���ʽΪy=kx+n�����ô���ϵ����������ý���ʽ��Ȼ����y=0���������m��ֵ�����ݹ��ɶ������C��D�ij����ɣ���3���ȸ���������ͼ�Σ�������P�͵�Q��λ�ã�Ȼ������ƽ���ߵ����ʣ����������ϵ�������ص���������P�����꣮
���  �⣺��1���ߒ�����y=-$\frac{1}{2}$x2+bx+4��ֱ��y=kx+4���ڵ�C��
�⣺��1���ߒ�����y=-$\frac{1}{2}$x2+bx+4��ֱ��y=kx+4���ڵ�C��
��C��0��4����
��OC=4��
��tan��OCA=$\frac{1}{2}$��
��A��-2��0����
����y=-$\frac{1}{2}$x2+bx+4���b=1��
�������ߵĽ���ʽΪy=-$\frac{1}{2}$x2+x+4��
��y=0����0=-$\frac{1}{2}$x2+x+4�����x=-2��x=4��
��B��4��0����
��AB=6��
���ACB�����=$\frac{1}{2}$AB•OC=$\frac{1}{2}$��6��4=12��
��2����y=-$\frac{1}{2}$x2+x+4=-$\frac{1}{2}$��x-1��2+$\frac{9}{2}$��
��D��1��$\frac{9}{2}$����
��ͼ��ֱ��y=3��Ȼ������C����ֱ��y=3�ĶԳƵ�C�䣬����C��D����ֱ��y=3��M��M��Ϊ����MC+MD����Сֵ����C��D�ij���
��C��0��4����
��C�䣨0��2����
��ֱ��C��D�Ľ���ʽΪy=kx+n��
��$\left\{\begin{array}{l}{n=2}\\{k+n=\frac{9}{2}}\end{array}\right.$���$\left\{\begin{array}{l}{k=\frac{5}{2}}\\{n=2}\end{array}\right.$��
��ֱ��C��D�Ľ���ʽΪy=$\frac{5}{2}$x+2��
��y=3�����3=$\frac{5}{2}$x+2�����x=$\frac{2}{5}$��
��M��$\frac{2}{5}$��3����
��m=$\frac{2}{5}$��
��C��D=$\sqrt{��1-0��^{2}+��\frac{9}{2}-2��^{2}}$=$\frac{\sqrt{29}}{2}$��
�࣬MC+MD����СֵΪ$\frac{\sqrt{29}}{2}$��
��3���������������������ĵ�Q��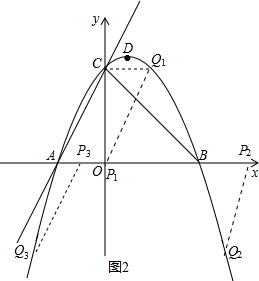
�ٵ���Q��Q1λ��ʱ��Q1��������Ϊ4�����������߿ɵõ�Q1������Ϊ��2��4����
��OA=2��
��P1��������0��0������
�ڵ���Q�ڵ�Q2λ��ʱ����Q2��������Ϊ-4�����������߿ɵõ�Q2����Ϊ��1+$\sqrt{17}$��-4����
��OA=2��
��P2��������3+$\sqrt{17}$��0������
�۵���Q��Q3λ��ʱ����Q3��������Ϊ-3�����������߽���ʽ�ɵã���Q3������Ϊ��1-$\sqrt{17}$��-4��
��OA=2��
��P3��������3-$\sqrt{17}$��0������
���Ͽɵ���������ĵ�P���������ֱ�Ϊ��P1��0��0����P2��3+$\sqrt{17}$��0����Q3��3-$\sqrt{17}$��0����
���� ���⿼���˶��κ������ۺ�Ӧ�ã�����ϵ���������ʽ����ԳƵ������Լ����·�����⣬ƽ���ı��ε����ʣ��������Ҫ������������֪ʶ������ݣ�����̽����Ŀ����������


 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
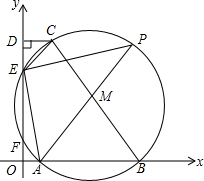 ��ƽ��ֱ������ϵ�У���BCΪֱ���ġ�M��x���������ڵ�A��B����y���������ڵ�E��F����CD��y����D����AM���ӳ�����M�ڵ�P������PE��AF��
��ƽ��ֱ������ϵ�У���BCΪֱ���ġ�M��x���������ڵ�A��B����y���������ڵ�E��F����CD��y����D����AM���ӳ�����M�ڵ�P������PE��AF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 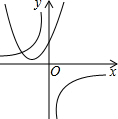 | B�� | 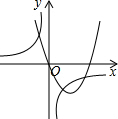 | C�� | 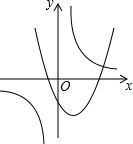 | D�� | 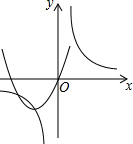 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
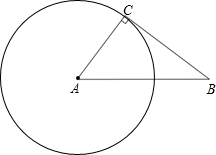 ��ͼ��Rt��ABC�У�AB=10cm��BC=8cm������C�ڡ�A�ϣ����A�İ뾶�ǣ�������
��ͼ��Rt��ABC�У�AB=10cm��BC=8cm������C�ڡ�A�ϣ����A�İ뾶�ǣ�������| A�� | 4cm | B�� | 6cm | C�� | 8cm | D�� | 10cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com