
分析 将分式的分子、分母去括号,除法化为乘法,然后再进行约分,使其分式到最简,再代值计算,代值时,要注意的是x的取值不能使原式的分母,除式为0.
解答 解:原式=$\frac{{x}^{4}{y}^{4}}{(x-y)^{8}}$•$\frac{{x}^{3}(x-y)^{3}}{{x}^{3}}$•$\frac{{x}^{4}}{{y}^{10}}$•$\frac{{y}^{5}(x-y)^{5}}{{x}^{5}}$=$\frac{{x}^{3}}{y}$,
把x=-2,y=4代入原式=$\frac{(-2)^{3}}{4}$=-2.
点评 本题考查了分式的化简求值.解答此题的关键是把分式化到最简,在化简过程中要细心不然很容易出错的.化到最简然后代值计算.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
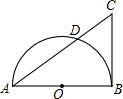 如图,AB是半圆O的直径,CB是半圆O的切线,B是切点,AC交半圆O于点D,已知CD=1,AD=4,则tan∠CAB=$\frac{1}{2}$.
如图,AB是半圆O的直径,CB是半圆O的切线,B是切点,AC交半圆O于点D,已知CD=1,AD=4,则tan∠CAB=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
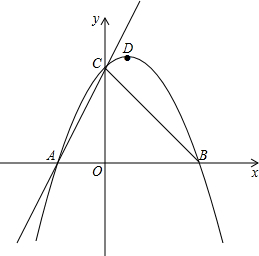 如图,在平面直角坐标系中,拋物线y=-$\frac{1}{2}$x2+bx+4与直线y=kx+4交于点A、C,与x轴交于点A、B,点A在原点左侧,点D是该拋物线的顶点.已知tan∠OCA=$\frac{1}{2}$,连接CB.
如图,在平面直角坐标系中,拋物线y=-$\frac{1}{2}$x2+bx+4与直线y=kx+4交于点A、C,与x轴交于点A、B,点A在原点左侧,点D是该拋物线的顶点.已知tan∠OCA=$\frac{1}{2}$,连接CB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com