
分析 (1)由AD=AC,BC=BE,根据等边对等角得出∠ACD=∠ADC,∠BCE=∠BEC,再利用三角形内角和定理得出∠ACD=(180°-∠A)÷2,∠BCE=(180°-∠B)÷2,而∠A+∠B=90°,那么求出∠ACD+∠BCE=135°,则∠DCE=∠ACD+∠BCE-∠ACB=90°;
(2)由AD=AC,BC=BE,根据等边对等角得出∠ACD=∠ADC,∠BCE=∠BEC,再利用三角形内角和定理得出∠ACD=(180°-∠CAD)÷2,∠BCE=(180°-∠CBE)÷2,而∠CAD+∠CBE=220°,那么求出∠ACD+∠BCE=70°,则∠DCE=∠ACD+∠BCE+∠ACB=110°;
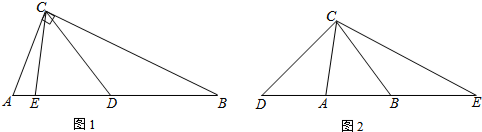
(3)分四种情况进行讨论:①点D、E在边AB上,同(1)可求出∠DCE=90°-$\frac{1}{2}$n°;②点D在BA延长线上,点E在AB延长线上,同(2)可求出∠DCE=90°+$\frac{1}{2}$n°;③点D在边AB上,点E在AB延长线上,求出∠DCE=$\frac{1}{2}$n°;④点D在BA延长线上,点E在边AB上,求出∠DCE=$\frac{1}{2}$n°.
解答 解:(1)∵AD=AC,BC=BE,
∴∠ACD=∠ADC,∠BCE=∠BEC,
∴∠ACD=(180°-∠A)÷2,∠BCE=(180°-∠B)÷2,
∵∠A+∠B=90°,
∴∠ACD+∠BCE=180°-(∠A+∠B)÷2=180°-45°=135°,
∴∠DCE=∠ACD+∠BCE-∠ACB=135°-90°=45°;
(2)∵AD=AC,BC=BE,
∴∠ACD=∠ADC,∠BCE=∠BEC,
∴∠ACD=(180°-∠CAD)÷2,∠BCE=(180°-∠CBE)÷2,
∵∠CAD+∠CBE=180°-∠CAB+180°-∠ABC=360°-(180°-∠ACB)=180°+40°=220°,
∴∠ACD+∠BCE=(180°-∠CAD)÷2+(180°-∠CBE)÷2=180°-(∠CAD+∠CBE)÷2=180°-220°÷2=70°,
∴∠DCE=∠ACD+∠BCE+∠ACB=70°+40°=110°.
故答案为110°;
(3)分四种情况进行讨论:
①点D、E在边AB上,
∵AD=AC,BC=BE,
∴∠ACD=∠ADC,∠BCE=∠BEC,
∴∠ACD=(180°-∠A)÷2,∠BCE=(180°-∠B)÷2,
∵∠A+∠B=180°-n°,
∴∠ACD+∠BCE=180°-(∠A+∠B)÷2=180°-90°+$\frac{1}{2}$n°=90°+$\frac{1}{2}$n°,
∴∠DCE=∠ACD+∠BCE-∠ACB=90°+$\frac{1}{2}$n°-n°=90°-$\frac{1}{2}$n°;
②点D在BA延长线上,点E在AB延长线上,
∵AD=AC,BC=BE,
∴∠ACD=∠ADC,∠BCE=∠BEC,
∴∠ACD=(180°-∠CAD)÷2,∠BCE=(180°-∠CBE)÷2,
∵∠CAD+∠CBE=180°-∠CAB+180°-∠ABC=360°-(180°-∠ACB)=180°+n°,
∴∠ACD+∠BCE=(180°-∠CAD)÷2+(180°-∠CBE)÷2=180°-(∠CAD+∠CBE)÷2=180°-90°-$\frac{1}{2}$n°=90°-$\frac{1}{2}$n°,
∴∠DCE=∠ACD+∠BCE+∠ACB=90°-$\frac{1}{2}$n°+n°=90°+$\frac{1}{2}$n°;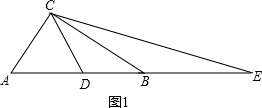 ③如图1,点D在边AB上,点E在AB延长线上,
③如图1,点D在边AB上,点E在AB延长线上,
∵AD=AC,BC=BE,
∴∠ACD=∠ADC,∠BCE=∠BEC,
∴∠ACD=(180°-∠CAD)÷2,∠BCE=(180°-∠CBE)÷2,
∵∠CBE=∠CAD+∠ACB=∠CAD+n°,
∴∠CAD-∠CBE=-n°,
∴∠DCE=∠DCB+∠BCE=∠ACB-∠ACD+∠BCE=n°-(180°-∠CAD)÷2+(180°-∠CBE)÷2=n°+(∠CAD-∠CBE)÷2=n°-$\frac{1}{2}$n°=$\frac{1}{2}$n°;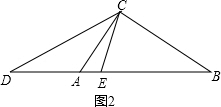 ④如图2,点D在BA延长线上,点E在边AB上,
④如图2,点D在BA延长线上,点E在边AB上,
∵AD=AC,BC=BE,
∴∠ACD=∠ADC,∠BCE=∠BEC,
∴∠ACD=(180°-∠CAD)÷2,∠BCE=(180°-∠CBE)÷2,
∵∠CAD=∠CBE+∠ACB=∠CBE+n°,
∴∠CBE-∠CAD=-n°,
∴∠DCE=∠DCA+∠ACE=∠ACD+∠ACB-∠BCE=n°+(180°-∠CAD)÷2-(180°-∠CBE)÷2=n°+(∠CBE-∠CAD)÷2=n°-$\frac{1}{2}$n°=$\frac{1}{2}$n°.
点评 本题考查了等腰三角形的性质,三角形内角和定理,运用数形结合、分类讨论是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
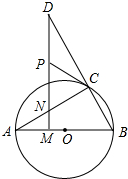 如图所示,△ABC的外接圆圆心O在AB上,点D是BC延长线上一点,DM⊥AB于M,交AC于N,且AC=CD.CP是△CDN的边ND上的中线.
如图所示,△ABC的外接圆圆心O在AB上,点D是BC延长线上一点,DM⊥AB于M,交AC于N,且AC=CD.CP是△CDN的边ND上的中线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
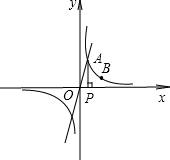 已知正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为P点,已知△OAP的面积为1.
已知正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为P点,已知△OAP的面积为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
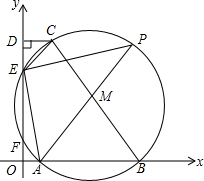 在平面直角坐标系中,以BC为直径的⊙M交x轴正半轴于点A、B,交y轴正半轴于点E、F,作CD⊥y轴于D连接AM并延长交⊙M于点P,连接PE、AF.
在平面直角坐标系中,以BC为直径的⊙M交x轴正半轴于点A、B,交y轴正半轴于点E、F,作CD⊥y轴于D连接AM并延长交⊙M于点P,连接PE、AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com