
 如图,在矩形ABCD中,AB=2$\sqrt{3}$,BC=6,将该矩形沿对角线BD翻折,C的对应点为G,使△DBG与△DBC在同一平面内,BG交AD于点E,在DA延长线上取点F,使AE=AF,连接BF.
如图,在矩形ABCD中,AB=2$\sqrt{3}$,BC=6,将该矩形沿对角线BD翻折,C的对应点为G,使△DBG与△DBC在同一平面内,BG交AD于点E,在DA延长线上取点F,使AE=AF,连接BF.分析 (1)根据SAS得出△FAB≌△EAB后,得出BF=BE,得出△BEF是等腰三角形;
(2)根据全等三角形判定出△DGE≌△EAB,再根据勾股定理得出EG的长度即可;
(3)根据△BAF沿射线BD方向的平移分情况进行求解,同时根据三角形的面积公式进行分析解答.
解答 解:(1)在△FAB和△EAB中,
$\left\{\begin{array}{l}{AE=AF}\\{∠EAB=∠FAB=90°}\\{AB=AB}\end{array}\right.$,
∴△FAB≌△EAB(SAS),
∴BE=BF,
∴△BEF是等腰三角形,
故答案为:等腰三角形;
(2)∵矩形沿对角线BD翻折,
∴△BDC≌△BDG,
∴DG=DC=AB,
在△EBA和△EDG中,
$\left\{\begin{array}{l}{∠AEB=∠GED}\\{∠EAB=∠EGD=90°}\\{DG=BA}\end{array}\right.$,
∴△DGE≌△EAB(AAS),
∴BE=DE,AE=EG,
在Rt△GED中,
EG2+DG2=DE2,即$E{G}^{2}+(2\sqrt{3})^{2}=(6-EG)^{2}$,
解得:EG=2;
(3)①当$0<t≤\sqrt{3}$时,△BAF沿射线BD方向的平移图如图1,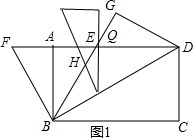
∴HQ=HP=BPtan30°=$\frac{2\sqrt{3}t}{3}$,
∴$S={S}_{△HQP}=\frac{1}{2}×\frac{1}{2}H{Q}^{2}×\sqrt{3}=\frac{\sqrt{3}}{3}{t}^{2}$,
②当$\sqrt{3}<t≤\frac{3\sqrt{3}}{2}$时,△BAF沿射线BD方向的平移图如图2,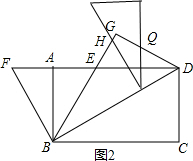
∴${S}_{△BAP}=\frac{1}{2}B{P}^{2}×\frac{\sqrt{3}}{3}=\frac{\sqrt{3}}{6}B{P}^{2}$,
${S}_{△QPD}=\frac{\sqrt{3}}{4}P{D}^{2}$,
${S}_{△BGD}=\frac{1}{2}×6×2\sqrt{3}=6\sqrt{3}$,
∴$S={S}_{△BGD}-{S}_{△BHP}-{S}_{△QPD}=-\frac{5\sqrt{3}}{3}{t}^{2}+12t-6\sqrt{3}$,
③当$\frac{3\sqrt{3}}{2}<t<2\sqrt{3}$时,△BAF沿射线BD方向的平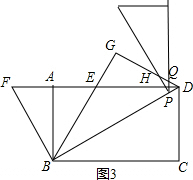 移图如图3,
移图如图3,
∴${S}_{△HPQ}=\frac{1}{2}P{D}^{2}×\sqrt{3}=\frac{\sqrt{3}}{2}P{D}^{2}$,
∴$S={S}_{△HPQ}-{S}_{△QPD}=\sqrt{3}{t}^{2}-12t+12\sqrt{3}$,
综上所述:S与t的函数关系式为:$\left\{\begin{array}{l}{S=\frac{\sqrt{3}}{3}{t}^{2}(0<t≤\sqrt{3})}\\{S=-\frac{5\sqrt{3}}{3}{t}^{2}+12t-6\sqrt{3}(\sqrt{3}<t≤\frac{3\sqrt{3}}{2})}\\{S=\sqrt{3}{t}^{2}-12t+12\sqrt{3}(\frac{3\sqrt{3}}{2}<t<2\sqrt{3})}\end{array}\right.$.
点评 此题考查几何变换问题,关键是全等三角形的判定和性质,同时注意平移的性质,综合性强,是一道典型题目.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
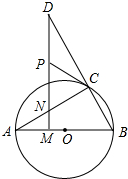 如图所示,△ABC的外接圆圆心O在AB上,点D是BC延长线上一点,DM⊥AB于M,交AC于N,且AC=CD.CP是△CDN的边ND上的中线.
如图所示,△ABC的外接圆圆心O在AB上,点D是BC延长线上一点,DM⊥AB于M,交AC于N,且AC=CD.CP是△CDN的边ND上的中线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
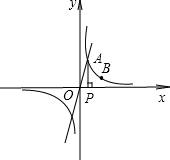 已知正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为P点,已知△OAP的面积为1.
已知正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为P点,已知△OAP的面积为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
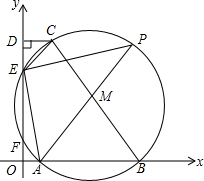 在平面直角坐标系中,以BC为直径的⊙M交x轴正半轴于点A、B,交y轴正半轴于点E、F,作CD⊥y轴于D连接AM并延长交⊙M于点P,连接PE、AF.
在平面直角坐标系中,以BC为直径的⊙M交x轴正半轴于点A、B,交y轴正半轴于点E、F,作CD⊥y轴于D连接AM并延长交⊙M于点P,连接PE、AF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com