
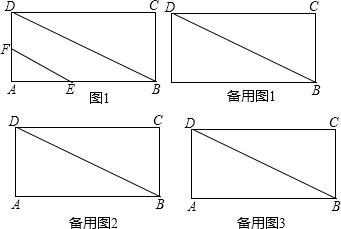
���� ��1�����ݡ�AEF�ס�ADB����֤��EF��BD��
��2����EFƽ�Ƶ�A��BD�Ĵ��߶ε��е�ʱ����E��AB���е�ʱ��P����BD�ϣ�
��3����0��t��2ʱ���غϲ��ֵ��ڡ�AEF�������
��2��t��4ʱ�����ݡ�PEF�ס�PGH���������������ε�����ıȵ������Ʊȵ�ƽ����á�PGH����������غϲ��ֵ����������ã�Ȼ�����ö��κ��������������ֵ��
��4����AB����ֱ��Ϊx�ᣬ��AD����ֱ��Ϊy�ᣬ��E�������ǣ�2t��0����F�������ǣ�0��t����EF��Բ��ֱ����EF���е���Բ�ģ���������ʱԲ�ĵ�ֱ�ߵľ�����ڰ뾶������⣮
��� �⣺��1��EF��BD�Ĺ�ϵ��EF��BD��
���ǣ�ƽ�У�
��2����t=2ʱ��E��F�ֱ���AB��AD���е㣬��EF��BD����A�ĶԳƵ�P����BD�ϣ�
�ʴ��ǣ�2��
��3����0��t��2ʱ���غϲ��ֵ��ڡ�AEF���������y=$\frac{1}{2}$��2t•t=t2����t=2ʱ�����ֵ��4��
��2��t��4ʱ����ͼ1��������AP��BD�ڵ�M��
��ֱ�ǡ�ABD�У�BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$��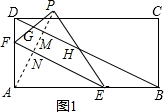
��AM=$\frac{AB•AD}{BD}$=$\frac{8��4}{4\sqrt{5}}$=$\frac{8\sqrt{5}}{5}$��
ͬ��AN=$\frac{2\sqrt{5}}{5}$t��
��PM=PN-MN=AN-MN=$\frac{2\sqrt{5}}{5}$t-��$\frac{8\sqrt{5}}{5}$-$\frac{2\sqrt{5}}{5}$t��=$\frac{4\sqrt{5}}{5}$t-$\frac{8\sqrt{5}}{5}$��
��EF��BD��
���PMN�ס�PEF��
��$\frac{{S}_{��PGH}}{{S}_{��PEF}}$=��$\frac{PM}{PN}$��2=��$\frac{PM}{AN}$��2=��2-$\frac{4}{t}$��2��
��S��PGH=t2��2-$\frac{4}{t}$��2=4t2-16t+16��
��y=t2-��4t2-16t+16������y=-3t2+16t-16��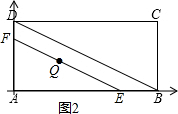 ��t=$\frac{8}{3}$ʱ��y�����ֵ�ǣ�$\frac{16}{3}$��
��t=$\frac{8}{3}$ʱ��y�����ֵ�ǣ�$\frac{16}{3}$��
��֮����t=$\frac{8}{3}$ʱ��y�����ֵ�ǣ�$\frac{16}{3}$��
��3����ͼ2����AB����ֱ��Ϊx�ᣬ��AD����ֱ��Ϊy�ᣬ��E�������ǣ�2t��0����F�������ǣ�0��t����
��EF���е�Q�������ǣ�t��$\frac{1}{2}$t����EF=$\sqrt{5}$t����Բ�İ뾶��$\frac{\sqrt{5}}{2}$t��
��Բ��CD����ʱ��4-$\frac{1}{2}$t=$\frac{\sqrt{5}}{2}$t����ã�t=2��$\sqrt{5}$+1����
���� ���⿼����ͼ�ε��۵��Լ����������ε��ж������ʣ����������ε�����ıȵ������Ʊȵ�ƽ�������PM�ij��DZ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
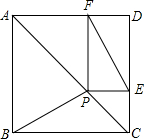 ������ABCD�У���P�ǶԽ���AC��һ�㣬PE��CD��E��PF��AD��F��
������ABCD�У���P�ǶԽ���AC��һ�㣬PE��CD��E��PF��AD��F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
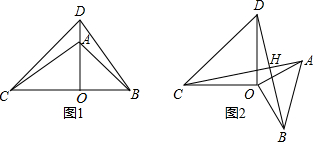 ��ͼ����AOB���COD���ǵ���ֱ�������Σ�
��ͼ����AOB���COD���ǵ���ֱ�������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com