
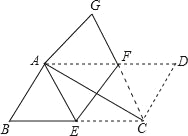
【题目】如图,将ABCD沿EF折叠,恰好使点C与点A重合,点D落在点G处,连接AC、CF.
(1)求证:△ABE≌△AGF.
(2)判断四边形AECF的形状,说明理由.
【答案】(1)详见解析;(2)边形AECF是菱形,理由详见解析.
【解析】分析:(1)由四边形ABCD是平行四边形与折叠性质,易得AB=AG,∠BAE=∠GAF,∠BEA=∠EAF=∠GFA,则可利用AAS判定:△ABE≌△AGF.
(2)由(1)易证得EC=AE=AF,又由AF∥EC,即可判定四边形AECF是菱形.
详解:(1)∵四边形ABCD是平行四边形,∴AB=CD,∠BAD=∠BCD,由折叠的性质得:AG=CD,∠EAG=∠BCD,∴AB=AG,∠BAD=∠EAG,∴∠BAE=∠GAF.
又∵AB∥CD,AE∥GF,AD∥BC,∴∠BEA=∠EAF=∠GFA.在△ABE和△AGF中,∵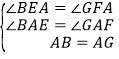 ,∴△ABE≌△AGF(AAS);
,∴△ABE≌△AGF(AAS);
(2)四边形AECF是菱形.理由如下:
由折叠的性质得:EC=AE.
∵△ABE≌△AGF,∴AE=AF,∴EC=AE=AF.
∵AF∥EC,∴四边形AECF是平行四边形,∴AECF是菱形.


科目:初中数学 来源: 题型:
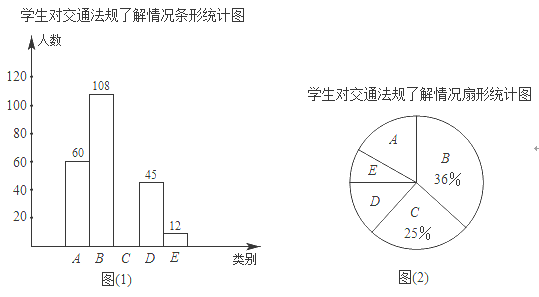
【题目】“机动车行驶到斑马线要礼让行人”等交通法规实施后,某校数学课外实践小组就对这些交通法规的了解情况在全校随机调査了部分学生,调查结果分为五种:A非常了解,B比较了解,C基本了解,D不太了解,E完全不知.实践小组把此次调查结果整理并绘制成下面不完整的条形统计图和扇形统计图请根据以上信息,解答下列问题:
(1)本次共调查了 名学生,扇形统计图中D所对应扇形的圆心角为 度;
(2)把这幅条形统计图补充完整(画图后请标注相应的数据);
(3)该校共有800名学生,根据以上信息,请你估计全校学生中对这些交通法规“非常了解”的有 名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图中有四条互相不平行的直线L1、L2、L3、L4所截出的七个角.关于这七个角的度数关系,下列何者正确( )
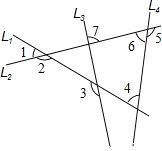
A. ∠2=∠4+∠7 B. ∠3=∠1+∠6 C. ∠1+∠4+∠6=180° D. ∠2+∠3+∠5=360°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
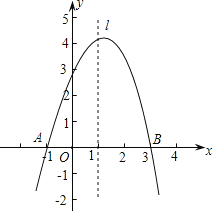
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是直线CD上一点,OA, OB分别平分∠COE,∠DOE,
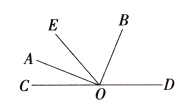
(1)写出以O为顶点的2个角(除∠COE,∠DOE外)
(2)求∠AOB的度数
(3)如果![]() :
:![]() =1:3,求∠AOC和∠BOD的度数。
=1:3,求∠AOC和∠BOD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
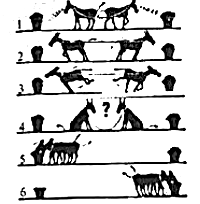
【题目】用同样大小的围棋子按如图所示的方式摆图案,按照这样的规律摆下去,第12个图案的围棋子个数是( )

A. 16 B. 28 C. 29 D. 38
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
A.放下自我,彼此尊重; B.放下利益,彼此平衡;
C.放下性格,彼此成就; D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟.根据同学们的选择情况,小明绘制了下面两幅不完整的图表,请根据图表中提供的信息,解答下列问题:

(1)参加本次讨论的学生共有 人;
(2)表中![]() ,
,![]() ;
;
(3)将条形统计图补充完整;
(4)现准备从![]() 四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点
四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点![]() (合理竞争,合作双赢)的概率.
(合理竞争,合作双赢)的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
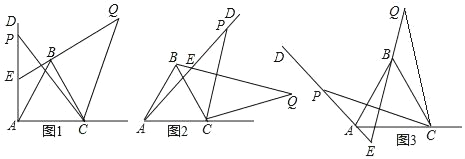
【题目】如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E.
(1)如图1,猜想∠QEP= °;
(2)如图2,3,若当∠DAC是锐角或钝角时,其它条件不变,猜想∠QEP的度数,选取一种情况加以证明;
(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
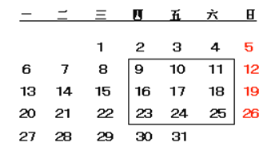
【题目】如图:是某月份的月历表,请你认真观察月历表,回答以下问题:
(1)如果圈出同一行的三个数,用a表示中间的数,则第一个数,第三个数怎样表示?
(2)如果圈出同一列的三个数,用a表示中间的数,则第一个数,第三个数怎样表示?
(3)如果圈出如图所示的任意9个数,这9个数的和可能是207吗?如果可能,请求出这9个数;如果不可能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com