
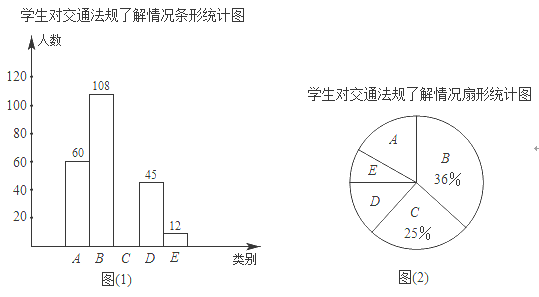
����Ŀ������������ʻ��������Ҫ�������ˡ��Ƚ�ͨ����ʵʩ��ijУ��ѧ����ʵ��С��Ͷ���Щ��ͨ������˽������ȫУ��������˲���ѧ������������Ϊ���֣�A�dz��˽⣬B�Ƚ��˽⣬C�����˽⣬D��̫�˽⣬E��ȫ��֪��ʵ��С��Ѵ˴ε��������������Ƴ����治����������ͳ��ͼ������ͳ��ͼ�����������Ϣ������������⣺
��1�����ι��������� ����ѧ��������ͳ��ͼ��D����Ӧ���ε�Բ�Ľ�Ϊ�� ���ȣ�
��2�����������ͳ��ͼ������������ͼ�����ע��Ӧ�����ݣ���
��3����У����800��ѧ��������������Ϣ���������ȫУѧ���ж���Щ��ͨ���桰�dz��˽⡱������ ������
���𰸡���1��300��54����2������ͳ��ͼ�����������(3) 160.
��������
��1��������ͳ��ͼ�У��ɵõ���B��������108�ˣ�������ͳ��ͼ�пɵá�B����ռ36%��������������ռ�İٷֱȼ���������������������D������ռ����İٷֱȣ���360��ȥ������ٷֱȼ��ɵó�D����Ӧ���ε�Բ�ĽǶ�����
��2�������������ԡ�C������ռ�ٷֱ������C������������ٲ�ȫͳ��ͼ��
��3�������A������ռ�İٷֱȣ�����������������м��㼴�ɣ�
��1��������ѧ������Ϊ��![]() ��300��
��300��
����D������![]() ��15%��Բ�Ľǣ�
��15%��Բ�Ľǣ�![]() ��54��
��54��
�ʴ�Ϊ��300��54��
��2��25%��300��75������ͳ��ͼ�������£�
(3)![]() ��800��160.
��800��160.
�ʴ�Ϊ��160��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��AC��BE��AC�ڵ�E��CF��AB�ڵ�F��BE��CF���ڵ�D�������н����в���ȷ����(����)

A. ��ABE�ա�ACF B. ��D����BAC��ƽ������
C. ��BDF�ա�CDE D. D��BE���е�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����λ��Ȼ��m����������������λ�ϵ����ֶԵ����һ����λ��Ϊ0 ������λ��Ȼ�� m���� m��������m��ͬ������m��=![]() ���� m�� ���еĿ�������У���|a+2b-c| ��Сʱ�����dzƴ�ʱ��m�� ��m �����Ҹ��������������涨K (m) = a2 +2b2 -c2�����磺318�����������ɵ������У�381��813 ��138 ����Ϊ|3+2
���� m�� ���еĿ�������У���|a+2b-c| ��Сʱ�����dzƴ�ʱ��m�� ��m �����Ҹ��������������涨K (m) = a2 +2b2 -c2�����磺318�����������ɵ������У�381��813 ��138 ����Ϊ|3+2![]() 8��1���� 18 ����8+ 2
8��1���� 18 ����8+ 2![]() 1��3����7����1 +2
1��3����7����1 +2![]() 3��8����1��1< 7<18 ������138 ��318�����Ҹ�����������K(318)=|12+2
3��8����1��1< 7<18 ������138 ��318�����Ҹ�����������K(318)=|12+2![]() 32��82|=��45��
32��82|=��45��
��1������λ��Ȼ��t�İ�λ�ϵ�������ʮλ�ϵ����ֶ�Ϊn��1��n �� 9 ��nΪ��Ȼ��������λ�ϵ�����Ϊ0 ����֤��K (t )�� 0��
��2������λ��Ȼ��s��100+10x + y(1�� x �� 9,1��y��9, ,x y Ϊ��Ȼ��) ����x<y ���������λ��ʮλ�ϵ����ֵõ�����s������19s+8s��=3888����ô���dz�sΪ����
��������������������������������K (s )�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ʊ�۸�涨���±���
��Ʊ���� | 1~50�� | 51~100�� | 100������ |
ÿ��Ʊ�ļ۸� | 15Ԫ | 13Ԫ | 11Ԫ |
ijУ���꼶(1)(2)�����102��ȥ��������(1)�೬��40�ˣ�����50�ˣ������㣬����������Ϊ��λ��Ʊ����һ��Ӧ��1422Ԫ.�ʣ�
(1)��������ж���ѧ����
(2)���������������������Ϊһ�����幺Ʊ���ɱ��������Ϊ��λ��Ʊʡ����ԪǮ��
(2)������꼶(1)�����֯ȥ������Ϊ��֯�ߵ�����ι�Ʊ����ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��y����x��b�ֱ���x��y�ύ��A��6��0����B���㣮
��1����ֱ��AB�Ľ���ʽ��
��2����PΪA���Ҳ�x���ϵ�һ���㣬��PΪֱ�Ƕ��㣬BPΪ���ڵ�һ������������ֱ�ǡ�BPQ������QA���ӳ���y���ڵ�K����P���˶�ʱ��K���λ���Ƿ����仯�������䣬������������ꣻ����仯����˵�����ɣ�
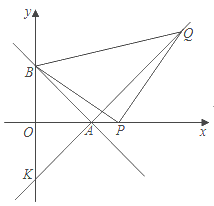
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���֪��BAD=120�㣬��EGF=60��, ��EGF�Ķ���G�����ζԽ���AC���˶����ǵ����߷ֱ�BC��CD��E��F��
[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/STEM/6b570bc424f747a8be031e9f971720ec.png]
��1����ͼ�ף�������G�˶������A�غ�ʱ����֤��EC+CF=BC��
��2��֪ʶ̽����
����ͼ�ң�������G�˶���AC���е�ʱ����ֱ��д���߶�EC��CF��BC��������ϵ������Ҫд��֤�����̣���
����ͼ�����ڶ���G�˶��Ĺ����У���![]() ��̽���߶�EC��CF��BC��������ϵ��
��̽���߶�EC��CF��BC��������ϵ��
��3������������ͼ������֪���εı߳�Ϊ8��BG=7��CF=![]() ����
����![]() ��2ʱ����EC�ij��ȡ�
��2ʱ����EC�ij��ȡ�
[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/STEM/1671b8ec524a49feac7097357d4ff9a8.png]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ʾ�������˴�ͬһ���ص��������������10:00ʱ���״�Լ����13ǧ�ס�����ͼ��ش�
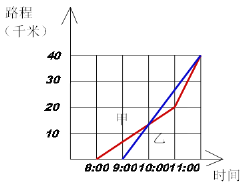
��1�����Ǽ����ӳ�����
��2�����Ǽ����ӳ�������ʮ��ʱ������Լ���˶���ǧ�ף�
��3����10:00Ϊֹ���ĸ��˵��ٶȿ죿
��4��������;���м����������ֱ��ڼ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD��EF�۵���ǡ��ʹ��C���A�غϣ���D���ڵ�G��������AC��CF��
��1����֤����ABE�ա�AGF��
��2���ж��ı���AECF����״��˵�����ɣ�
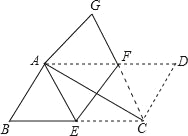
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com