
 如图,已知F、G是OA上两点,M、N是OB上两点,且FG=MN,S△PFG=S△PMN,试问:点P是否在∠AOB的平分线上?
如图,已知F、G是OA上两点,M、N是OB上两点,且FG=MN,S△PFG=S△PMN,试问:点P是否在∠AOB的平分线上?科目:初中数学 来源: 题型:
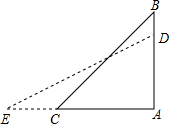 如图,有一直立标杆,它的上部被风从B处吹折,杆顶C着地,离杆脚2m,修好后又被风吹折,因新断处D比前一次低0.5m,故杆顶E着地比前次远1m,求原标杆的高度.
如图,有一直立标杆,它的上部被风从B处吹折,杆顶C着地,离杆脚2m,修好后又被风吹折,因新断处D比前一次低0.5m,故杆顶E着地比前次远1m,求原标杆的高度.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com