
如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)求证:AE•BC=BD•AC;
(2)如果S△ADE=3,S△BDE=2,DE=6,求BC的长.

考点: 相似三角形的判定与性质.
分析: (1)由BE平分∠ABC交AC于点E,ED∥BC,可证得BD=DE,△ADE∽△ABC,然后由相似三角形的对应边成比例,证得AE•BC=BD•AC;
(2)根据三角形面积公式与S△ADE=3,S△BDE=2,可得AD:BD=3:2,然后由平行线分线段成比例定理,求得BC的长.
解答: (1)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE.…(1分)
∵DE∥BC,
∴∠DEB=∠CBE…(1分)
∴∠ABE=∠DEB.
∴BD=DE,…(1分)
∵DE∥BC,
∴△ADE∽△ABC,
∴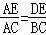 …(1分)
…(1分)
∴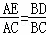 ,
,
∴AE•BC=BD•AC;…(1分)
(2)解:设△ABE中边AB上的高为h.
∴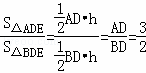 ,…(2分)
,…(2分)
∵DE∥BC,
∴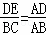 . …(1分)
. …(1分)
∴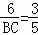 ,
,
∴BC=10. …(2分)
点评: 此题考查了相似三角形的判定与性质、平行线分线段成比例定理以及等腰三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.


科目:初中数学 来源: 题型:
对于一次函数y=﹣2x+4,下列结论错误的是( )
A.函数值随自变量的增大而减小
B.函数的图象不经过第三象限
C.函数的图象向下平移4个单位长度得y=﹣2x的图象
D.函数的图象与x轴的交点坐标是(0,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
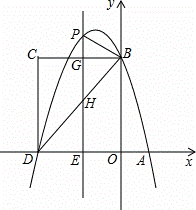
如图,在平面直角坐标系中,抛物线y=﹣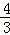 x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
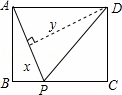
如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )
A.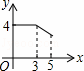 B.
B. C.
C. D.
D.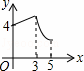
查看答案和解析>>
科目:初中数学 来源: 题型:
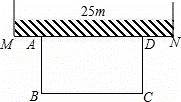
如图,某农场老板准备建造一个矩形羊圈ABCD,他打算让矩形羊圈的一面完全靠着墙MN,墙MN可利用的长度为25m,另外三面用长度为50m的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分)
(1)若要使矩形羊圈的面积为300m2,则垂直于墙的一边长AB为多少米?
(2)农场老板又想将羊圈ABCD的面积重新建造成面积为320m2,从而可以养更多的羊,请聪明 的你告诉他:他的这个想法能实现吗?为什么?
的你告诉他:他的这个想法能实现吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,两个同心圆的直径分别为6cm和10cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
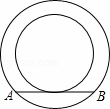
A. 4cm B. 6cm C. 8cm D. 10cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com