
如图,某农场老板准备建造一个矩形羊圈ABCD,他打算让矩形羊圈的一面完全靠着墙MN,墙MN可利用的长度为25m,另外三面用长度为50m的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分)
(1)若要使矩形羊圈的面积为300m2,则垂直于墙的一边长AB为多少米?
(2)农场老板又想将羊圈ABCD的面积重新建造成面积为320m2,从而可以养更多的羊,请聪明 的你告诉他:他的这个想法能实现吗?为什么?
的你告诉他:他的这个想法能实现吗?为什么?
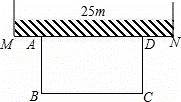
解:(1)设所围矩形ABCD的宽AB为x米,则宽AD为(50﹣2x)米.
依题意,得x•(50﹣2x)=300,
即,x2﹣25x+150=0,
解此方程,得x1=15,x2=10.
∵墙的长度不超过25m,
∴ x2=10不合题意,应舍去.
x2=10不合题意,应舍去.
∴垂直于墙的一边长AB为15米.
(2)不能.
因为由x•(50﹣2x)=320得x2﹣25x+160=0.
又∵b2﹣4ac=(25)2﹣4×1×160=﹣15<0,
∴上述方程没有实数根.
因此,不能使所围矩形场地的面积为320m2.
点评:此题考查了一元二次方程的应用,不仅是一道实际问题,而且结合了矩形的性质,解答此题要注意以下问题:
(1)矩形的一边为墙, 且墙的长度不超过45米;
且墙的长度不超过45米;
(2)根据矩形的面积公式列一元二次方程并根据根的判别式来判断是否两边长相等.


科目:初中数学 来源: 题型:
如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)求证:AE•BC=BD•AC;
(2)如果S△ADE=3,S△BDE=2,DE=6,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,以点P(﹣1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=2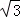 ,将△ABC绕点P旋转180°,得到△MCB.
,将△ABC绕点P旋转180°,得到△MCB.
(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;
(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com