
【题目】某商店以每件a元的价格购进30件甲种商品,以每件b元的价格购进40件乙种商品,且a<b.
(1)若该商店将甲种商品提价40%,乙种商品提价30%全部出售,则可获利多少元?(用含有a,b的式子表示结果)
(2)若该商店将两种商品都以![]() 元的价格全部出售,这次买卖该商店是盈利还是亏损,请说明理由?
元的价格全部出售,这次买卖该商店是盈利还是亏损,请说明理由?
【答案】(1)商店可获利(12 a+12b)元;(2)此次买卖该商店亏损,理由见解析.
【解析】试题分析:(1)因为获利=总卖价﹣总进价,用含a、b的代数式表示出总买价和总进价,计算其差即可;
(2)计算总买价与总进价的差得利润,再比较利润与0的关系判断盈亏.
试题解析:(1)总进价为:30a+40b
总售价为:(1+40%)a×30+( 1+30%)b×40
=42a+52b
∴商店获利为:(42a+52b)﹣(30a+40b)
=42a+52b﹣30a﹣40b
=12a+12b:
答:商店可获利(12 a+12b)元
(2)此次买卖该商店亏损,理由如下:
总售价为:(30+40)×![]() =35(a+b)
=35(a+b)
∴获利=35(a+b)﹣(30a+40b)
=35a+35b﹣30a﹣40b
=5a﹣5b
=5(a﹣b)
又∵a<b
∴a﹣b<0
∴5(a﹣b)<0
∴此次买卖该商店亏损.


 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】补全下列推理过程:
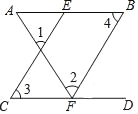
如图,已知∠1=∠2,∠3=∠4,试说明AB∥CD.
解:∵∠1=∠2(已知)
∴CE∥FB ( )
∴∠4=∠AEC ( )
∵∠3=∠4 ( 已知)
∴∠3=∠AEC ( )
∴AB∥CD( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两组邻边分别相等的四边形叫做筝形.如图1,四边形ABCD是一个筝形,其中AD=CD,AB=CB,我们称这个四边形是“筝形ABCD”.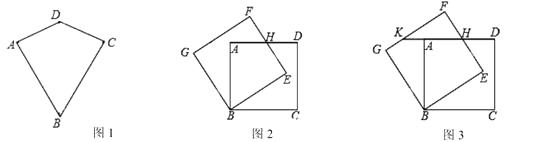
(1)根据筝形的定义判断下列命题是否正确,真命题打“√”,假命题打“×”.
①筝形有一组对角相等.
②菱形是筝形.
③筝形的面积为两条对角线长度的乘积.
(2)如图2,有一个公共顶点B的两个正方形ABCD与正方形BEFG全等,边AD与EF相交于点H.请你判断四边形BEHA是否是“筝形”,说明你的理由;
(3)如图3,当∠EBC=30°时,延长DA交GF于点K.若正方形ABCD边长为 ![]() ,求线段AK的长.
,求线段AK的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BD交AD于点E.已知AB=2,△DOE的面积为 ![]() ,则AE的长为( )
,则AE的长为( ) 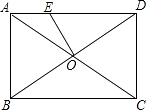
A.![]()
B.2
C.1.5
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对一批衬衣进行抽检,得到合格衬衣的频数表如下,若出售1200件衬衣,则其中次品的件数大约是( )
抽取件数(件) | 50 | 100 | 150 | 200 | 500 | 800 | 1000 |
合格频数 | 48 | 98 | 144 | 193 | 489 | 784 | 981 |
A.12B.24C.1188D.1176
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com