
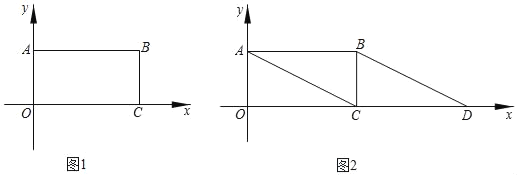
����Ŀ����ͼ��������AOCB�Ķ���A��m��n����C��p��q�����������ϣ���֪![]() ��
��![]() ���Ƿ���x+2y��4�������⣬��B�ڵ�һ�����ڣ�
���Ƿ���x+2y��4�������⣬��B�ڵ�һ�����ڣ�
��1�����B�����ꣻ
��2������P�ӵ�A������y�Ḻ���᷽����1����λÿ����ٶ��˶���ͬʱ��Q�ӵ�C��������x�Ḻ���᷽����2����λÿ����ٶ��˶������˶���������ʱ���ı���BPOQ���Ϊ������ABCO�����һ�룻
��3����ͼ2�����߶�AC��x��������ƽ�Ƶõ��߶�BD����E��a��b��Ϊ�߶�BD������һ�㣬����a+2b��ֵ�Ƿ�仯�����仯�����䷶Χ�������仯������ֵ����ֱ��д�����ۣ�
���𰸡���1����B������Ϊ��4��2������2���˶���1��ʱ���ı���BPOQ���Ϊ������ABCO�����һ�룻��3��a+2b��ֵ���仯��ֵΪ8.
��������
��1����������������ʰ�A,C���뷽��x+2y��4���õ��Ǹ������⣬�ٸ��ݾ��ε����ʼ��ɽ��.
��2����AP��t��CQ��2t���ٸ����ı���BPOQ�����������AOCB���������ABP���������BCQ��������t���ɽ��.
��3����EF��CD��F����ƽ�Ƶ���֤���ı���ABDC��ƽ���ı��Σ��ٸ���ƽ���ı��ε����ʵó�CD��AB��4��OD��OC+CD��8���ٸ��ݵ�E������Ϊ��a��b�����ó�OF��a��EF��b��DF��8��a������������������ε��ж������ʣ����ɽ��.
��1����A��m��n����C��p��q����
��m��0��n��0��p��0��q��0��
�߷���x+2y��4�ķǸ�������Ϊ![]() ��
��
��A��0��2����C��4��0����
���ı���AOCB�Ǿ��Σ�
��BC��OA��2��AB��OC��4��
���B��������4��2����
��2����ͼ1��ʾ��������ã�AP��t��CQ��2t��
���ı���BPOQ�����������AOCB���������ABP���������BCQ�������4��2��![]() ��4��t��
��4��t��![]() ��2t��2��
��2t��2��![]() ��4��2��
��4��2��
��ã�t��1��
���˶���1��ʱ���ı���BPOQ���Ϊ������ABCO�����һ�룻
��3��a+2b��ֵ���仯��ֵΪ8���������£�
��EF��CD��F����ͼ2��ʾ��
��EF��OA��BC��
��ƽ�Ƶ����ʵã�AC��BD��AC��BD��
���ı���ABDC��ƽ���ı��Σ�
��CD��AB��4��
��OD��OC+CD��8��
�ߵ�E������Ϊ��a��b����
��OF��a��EF��b��
��DF��8��a��
��EF��BC��
���DEF�ס�DBC��
��![]() ��
��
�����ã�a+2b��8��



 ����������ϵ�д�
����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
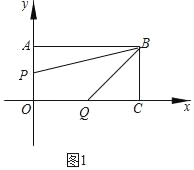
����Ŀ��ϣ����ѧ���꼶ѧ����չ����ӻ��ÿ����5��ѧ���μӣ��������ܷ��������Σ��ڹ涨ʱ����ÿ����100�����ϣ���100��Ϊ�������±��dzɼ��Ϻõļװ���Ұ�5��ѧ���ı����ɼ�����λ������
1�� | 2�� | 3�� | 4�� | 5�� | ���� | |
�װ� | 100 | 98 | 110 | 89 | 103 | 500 |
�Ұ� | 89 | 100 | 95 | 119 | 97 | 500 |
��ͳ�Ʒ�������5��ѧ������ӵ��ܸ����������ʱ��ѧ�����飬����ͨ�����������е�������Ϣ��Ϊ�ο�������ش��������⣺
��1��������������ݵ���λ����
��2����������������ݵķ�����Ƚ���һ��С��
��3������������Ϣ������ΪӦ�ðѹھ���״������һ���ࣿ��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ������Ȥ�С����Χ��һ���������ԣ�����һ�߿�ǽ�����������ó�Ϊ30�����Χ�ɣ���֪ǽ��Ϊ18��(��ͼ��ʾ)����������Դ�ֱ��ǽ��һ�߳�Ϊx�ף�
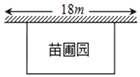
(1)�����Ե����Ϊ72ƽ���ף���x��ֵ��
(2)������Ե�����ܷ���120ƽ���ף���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2+bx+c��ͼ����x�ύ��A����5��0����B��1��0�����㣬��y�ύ�ڵ�C�������ߵĶԳ�����x�ύ�ڵ�D��
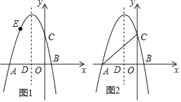
��1���������ߵĺ�������ʽ��
��2����ͼ1����E��x��y��Ϊ��������һ�㣬�ҩ�5��x����2������E��EF��x�ᣬ�������ߵĶԳ����ڵ�F����EH��x���ڵ�H���õ�����EHDF�������EHDF�ܳ������ֵ��
��3����ͼ2����PΪ�����߶Գ�����һ�㣬�Ƿ���ڵ�P��ʹ�Ե�P��A��CΪ�������������ֱ�������Σ������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ı߳�Ϊ4����ABΪһ�����ȱߡ�ABE��ʹ��E����������ABCD���ڲ�������AC��BE�ڵ�F������CE��DE��������˵���У��١�ADE�ա�BCE���ڡ�ACE=30�㣻��AF=![]() CF����
CF���� ![]() =2+
=2+![]() ��������ȷ���У�������
��������ȷ���У�������

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ٽ�����ڣ�ijʳƷ��ÿ������300ֻ���ӣ�����һֻ���ӵ�����Ϊ1Ԫ.�����鷢�֣����۵���ÿ��0.1Ԫ��ÿ��ɶ�����100ֻ����.Ϊ��ʹÿ���õ�������࣬�õ���������۵����½�m��0<m<1��Ԫ��
��1�����۵��۽��ۺ�ÿֻ����Ϊ Ԫ���õ�ÿ����۳� ֻ����.
��2���ڲ������������ص������£������۵����½�����Ԫʱ������ʹ�õ�ÿ���ȡ��������420Ԫ�������������Ӹ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�D��E�ֱ���AB��AC�ϵĵ㣬��AED=��ABC����BAC��ƽ����AF��DE�ڵ�G����BC�ڵ�F��
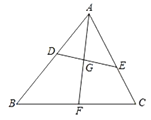
��1����д��ͼ�����е����������Σ�
��2����![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�������
�У�������![]() �ĵĶ���Ϊ
�ĵĶ���Ϊ![]() .
.
��1������![]() ������Ϊ .
������Ϊ .
��2���ᡢ�����궼�������ĵ��������.��![]()
![]() ����
����![]()
�ٵ�![]() ������Ϊ ��
������Ϊ ��
�ڹ���![]() ��
��![]() ��Ĵ���
��Ĵ���![]() ����ֱ��
����ֱ��![]() �������߽���
�������߽���![]() ���㣬����������
���㣬����������![]() ֮��IJ������߶�
֮��IJ������߶�![]() ��Χ�ɵ��������߽磩ǡ���߸����㣬��Ϻ���ͼ����
��Χ�ɵ��������߽磩ǡ���߸����㣬��Ϻ���ͼ����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BAD������BEC��ƽ�����Ƶ�B��ת60�����ã���AB��BC��BE��CE������DE.
��1����֤����BDE�ա�BCE��
��2�����ж��ı���ABED����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com