
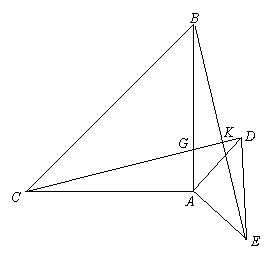
如图,△ABC和△AED是等腰直角三角形,∠BAC=∠EAD=90°,点D、E在∠BAC的外部,连结DC,BE.
(1)求证:BE=CD;
(2)若将△AED绕点A旋转,直线CD交直线AB于点G,交直线BE于点K.
①如果AC =8,GA=2,求GC·KG的值;
=8,GA=2,求GC·KG的值;
②当△BED为等腰直角三角形时,请你直接写出AB∶BD的值.
 |  | ||
解:(1)
证明:∵∠BAC=∠EAD=90°
∴∠BAC +∠BAD =∠EAD+∠BAD
∴∠CAD=∠BAE
在△BAE和△CAD中
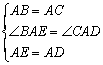
∴△BAE≌△CAD
∴BE=CD ………………………………………4分
(2)①当点G在线段AB上时(如图27-a)
∵△BAE≌△CAD ∴∠ACD=∠ABE
又∵∠CGA=∠BGK ∴△CGA∽△BGK
∴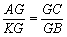 ∴
∴
∵AC=8 ∴AB=8
 ∵GA=2 ∴GB=6
∵GA=2 ∴GB=6
∴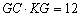 …………………………………7分
…………………………………7分
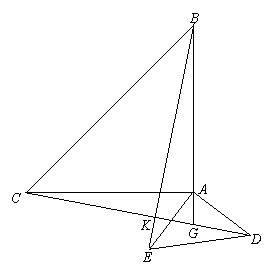
当点G在线段AB延长线上时(如图27-b )
)
∵△BAE≌△CAD ∴∠ACD=∠ABE
又∵∠BGK=∠CGA ∴△CGA∽△BGK
∴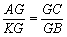 ∴
∴
|


科目:初中数学 来源: 题型:
如图①,底面积为30cm2的空圆柱形容器内水平放置着由两个实心圆柱组成的“几何体”,现向容器内匀速注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②所示.
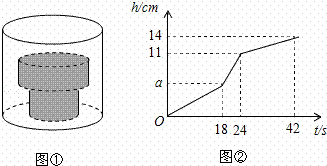
请根据图中提供的信息,解答下列问题:
(1)圆柱形容器的高为 cm,匀速注水的水流速度为 cm3/s;
(2)若“几何体”的下方圆柱的底面积为15cm2,求“几何体”上方圆柱的高和底面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
为了让学生了解党的十八大精神,某中学举行了一次“社会主义核心价值观暨八礼四仪知识竞赛”,共有1000名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:
(1)a= ,b= ;
(2)补全频数分布直方图;
(3)在该问题中的样本容量是多少? 答: .
(4)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为 人?
|
| ||
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | a | 0.20 |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | 12 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:
身高相同的三个小朋友甲、乙、丙放风筝,他们放出的线长分别为300 m,250 m,200 m;线与地面所成的角度分别为30°,45°,60°(假设风筝线是拉直的),则三人所放的风筝 ( )
A、甲的最高 B、乙的最低 C 、丙的最低 D、乙的最高
、丙的最低 D、乙的最高
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com