
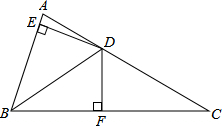
 如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,DE⊥AB(E在AB之间),DF⊥BC,已知BD=5,DE=3,CF=4,试求△DFC的周长.
如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,DE⊥AB(E在AB之间),DF⊥BC,已知BD=5,DE=3,CF=4,试求△DFC的周长. 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
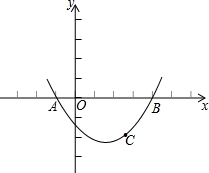 如图,已知抛物线过点A(-1,0),B(4,0),C(
如图,已知抛物线过点A(-1,0),B(4,0),C(| 11 |
| 5 |
| 12 |
| 5 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 几何体简称为体,按其形状可分为三类,即柱体、椎体、球体,下列图形中:
几何体简称为体,按其形状可分为三类,即柱体、椎体、球体,下列图形中:查看答案和解析>>
科目:初中数学 来源: 题型:
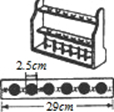 如图是学校化学实验室用于放试管的木架,在每层长29cm的木条上钻有6个圆孔,每个圆孔的直径均为2.5cm.两端与圆孔边缘及任何相邻两孔边缘之间的距离都相等并设为xcm,则x为
如图是学校化学实验室用于放试管的木架,在每层长29cm的木条上钻有6个圆孔,每个圆孔的直径均为2.5cm.两端与圆孔边缘及任何相邻两孔边缘之间的距离都相等并设为xcm,则x为查看答案和解析>>
科目:初中数学 来源: 题型:
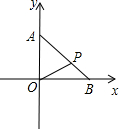 如图,点B,A分别在x,y轴的正半轴上,AB=m,且AP:PB=2:1,点B在x轴的正半轴上移动,线段AB的长保持不变.
如图,点B,A分别在x,y轴的正半轴上,AB=m,且AP:PB=2:1,点B在x轴的正半轴上移动,线段AB的长保持不变.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com