
【题目】阅读下面材料:
数学课上,老师给出了如下问题:
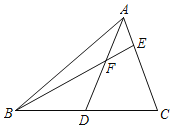
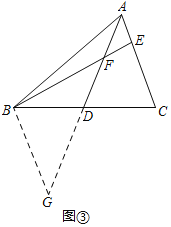
如图,AD为△ABC中线,点E在AC上,BE交AD于点F,AE=EF.求证:AC=BF.
经过讨论,同学们得到以下两种思路:
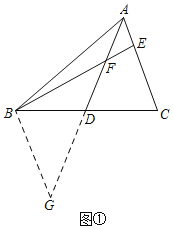
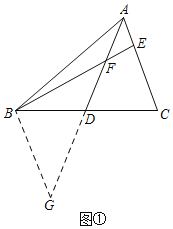
思路一如图①,添加辅助线后依据SAS可证得△ADC≌△GDB,再利用AE=EF可以进一步证得∠G=∠FAE=∠AFE=∠BFG,从而证明结论.
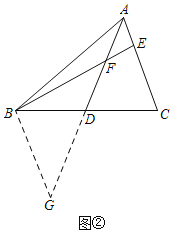
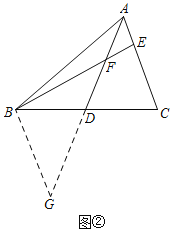
思路二如图②,添加辅助线后并利用AE=EF可证得∠G=∠BFG=∠AFE=∠FAE,再依据AAS可以进一步证得△ADC≌△GDB,从而证明结论.
完成下面问题:
(1)①思路一的辅助线的作法是: ;
②思路二的辅助线的作法是: .
(2)请你给出一种不同于以上两种思路的证明方法(要求:只写出辅助线的作法,并画出相应的图形,不需要写出证明过程).
【答案】(1)①延长AD至点G,使DG=AD,连接BG;②作BG=BF交AD的延长线于点G;(2)详见解析
【解析】
(1)①依据SAS可证得△ADC≌△GDB,再利用AE=EF可以进一步证得∠G=∠FAE=∠AFE=∠BFG,从而证明结论.
②作BG=BF交AD的延长线于点G.利用AE=EF可证得∠G=∠BFG=∠AFE=∠FAE,再依据AAS可以进一步证得△ADC≌△GDB,从而证明结论.
(2)作BG∥AC交AD的延长线于G,证明△ADC≌△GDB(AAS),得出AC=BG,证出∠G=∠BFG,得出BG=BF,即可得出结论.
解:(1)①延长AD至点G,使DG=AD,连接BG,如图①,理由如下:
∵AD为△ABC中线,
∴BD=CD,
在△ADC和△GDB中,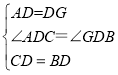 ,
,
∴△ADC≌△GDB(SAS),
∴AC=BG,
∵AE=EF,
∴∠CAD=∠EFA,
∵∠BFG=∠G,∠G=∠CAD,
∴∠G=∠BFG,
∴BG=BF,
∴AC=BF.
故答案为:延长AD至点G,使DG=AD,连接BG;
②作BG=BF交AD的延长线于点G,如图②.
理由如下:∵BG=BF,
∴∠G=∠BFG,
∵AE=EF,
∴∠EAF=∠EFA,
∵∠EFA=∠BFG,
∴∠G=∠EAF,
在△ADC和△GDB中,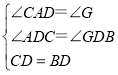 ,
,
∴△ADC≌△GDB(AAS),
∴AC=BG,
∴AC=BF;
故答案为:作BG=BF交AD的延长线于点G;
(2)作BG∥AC交AD的延长线于G,如图③所示:
则∠G=∠CAD,
∵AD为△ABC中线,
∴BD=CD,
在△ADC和△GDB中,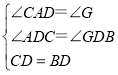 ,
,
∴△ADC≌△GDB(AAS),
∴AC=BG,
∵AE=EF,
∴∠CAD=∠EFA,
∵∠BFG=∠EFA,∠G=∠CAD,
∴∠G=∠BFG,
∴BG=BF,
∴AC=BF.


科目:初中数学 来源: 题型:
【题目】高新一中新图书馆在“校园书香四溢”活动中迎来了借书高潮,上周借书记录如下表:(超过100册的部分记为正,少于100册的部分记为负)
(1)上星期借书最多的一天比借书最少的一天多借出图书多少册?
(2)上星期平均每天借出多少册书?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并填空,如图:方格纸中每个小正方形的边长都为1,△ABC的顶点都在方格纸的格点上,将△ABC经过一次平移后得到△A'B'C'.图中标出了点C的对应点C'.
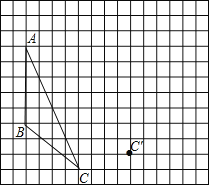
(1)请画出平移后的△A'B'C';
(2)若连接AA',BB',则这两条线段的关系是 ;
(3)利用网格画出△ABC中AC边上的中线BD以及AB边上的高CE;
(4)线段AB在平移过程中扫过区域的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2+(2m+1)x + m2﹣1与x轴交于A,B两个不同的点.
(1)求:m的取值范围;
(2)写出一个满足条件的m的值,并求此时A,B两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某翼装飞行员从离水平地面高AC=500m的A处出发,沿着俯角为15°的方向,直线滑行1600米到达D点,然后打开降落伞以75°的俯角降落到地面上的B点.求他飞行的水平距离BC(结果精确到1m).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(t﹣1,1)与点B关于过点(t,0)且垂直于x轴的直线对称.
(1)以AB为底边作等腰三角形ABC,
①当t=2时,点B的坐标为 ;
②当t=0.5且直线AC经过原点O时,点C与x轴的距离为 ;
③若![]() 上所有点到y轴的距离都不小于1,则t的取值范围是 .
上所有点到y轴的距离都不小于1,则t的取值范围是 .
(2)以AB为斜边作等腰直角三角形ABD,直线m过点(0,b)且与x轴平行,若直线m上存在点P,![]() 上存在点K,满足PK=1,直接写出b的取值范围.
上存在点K,满足PK=1,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点E,作BF⊥AM于点F,连接BE. 若AF=1,四边形ABED的面积为6,则BF的长为( )
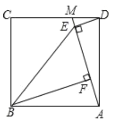
A.2B.3C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC.
(2)写出AB+AC与AE之间的等量关系,并说明理由.
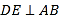
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com