
【题目】已知二次函数 y=(x-a-2)(x+a)+3.
(1)求该二次函数的图象的对称轴.
(2)对于该二次函数图象上的两点 P(x1,y1)、Q(x2,y2).
①当 x≥m 时,y 随 x 的增大而增大,写出一个符合条件的 m 值;
②当 m≤x2≤m+2,当 x1≤﹣1 时,均有 y1≥y2,求 m 的取值范围;
(3)当二次函数过(0,3)点时,且与直线 y=kx+2 交于 A、B 两点,其中有一交点的横坐标 x0 满足 1<x0<3, 求 k 的取值范围.
【答案】(1)x=1;(2)①m值可以为2;②-1≤m≤1;(3)![]()
【解析】
(1)首先把原二次函数化成y=(x-1)2-a2-2a+2,由此可得该二次函数的图象的对称轴;
(2)①根据二次函数的开口方向和对称轴可知y随x的增大而增大时,x的取值范围,从而可得符合条件的m值;
②首先得出当x1=-1,y1=y2时,x2=3,然后根据当x1≤-1时,均有y1≥y2,可得一个不等式组,解出即可;
(3)首先根据二次函数过(0,3)点,求出a的值,于是可得该二次函数的解析式,然后计算出直线x=1,直线x=3与二次函数y=x2-2x+3的交点坐标,得到直线DE的解析式为y=2,k1=0,设DF所在直线解析式为y=k2x+2,把(3,6)代入得k2=![]() 即可得出结论.
即可得出结论.
解:(1)因为y=(x-a-2)(x+a)+3,
∴y=(x-1)2-a2-2a+2,
∴该二次函数的图象的对称轴为x=1;
(2)①∵该二次函数开口向上,对称轴为x=1,
∴x≥1时,y随x的增大而增大,
∴m≥1的数都可以,
因此符合条件的m值可以为2;
②∵该二次函数的图象的对称轴为x=1,
∴当x1=-1,y1=y2时,x2=3,
∴当x1≤-1时,均有y1≥y2,
则-1≤x2≤3,
∴![]() ,
,
解得-1≤m≤1;
(3)当二次函数过(0,3)点时,
则有3=(0-1)2-a2-2a+2,
解得a=0或-2,
∴该二次函数的解析式为y=x2-2x+3,
如图:
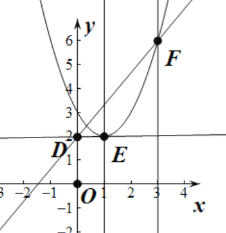
直线x=1,直线x=3分别与二次函数y=x2-2x+3交E、F两点,
易得E(1,2),F(3,6),
直线y=kx+2与y轴交于D点,D(0,2),
∵二次函数y=x2-2x+3与直线y=kx+2交于A、B两点,其中有一交点的横坐标![]() 满足1<x0<3,
满足1<x0<3,
直线y=kx+2与二次函数y=x2-2x+3的EF间有一交点,
直线DE的解析式为y=2,k1=0,设DF所在直线的解析式为y=k2x+2,把(3,6)代入得k2=![]() ,
,
∴k1<k<k2,即![]() .
.


科目:初中数学 来源: 题型:
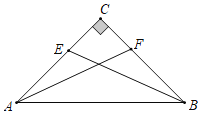
【题目】如图,等腰直角△ABC中,∠C=90°,AC=BC=![]() ,E、F为边AC、BC上的两个动点,且CF=AE,连接BE、AF,则BE+AF的最小值为_____.
,E、F为边AC、BC上的两个动点,且CF=AE,连接BE、AF,则BE+AF的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年5月的第二个星期日即为母亲节,“父母恩深重,恩怜无歇时”,许多市民喜欢在母亲节为母亲送花,感恩母亲,祝福母亲.今年节日前夕,某花店采购了一批鲜花礼盒,经分析上一年的销售情况,发现该鲜花礼盒的该周销售量y(盒)是销售单价x(元)的一次函数,已知销售单价为70元/盒时,销售量为160盒;销售单价为80元/盒时,销售量为140盒.
(1)求该周销售量y(盒)关于销售单价x(元)的一次函数解析式;
(2)若按去年方式销售,已知今年该鲜花礼盒的进价是每盒50元,商家要求该周至少要卖110盒,请你帮店长算一算,要完成商家的销售任务,销售单价不能超过多少元?
(3)在(2)的条件下,试确定销售单价x为何值时,花店该周销售鲜花礼盒获得的利润最大?并求出获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在建筑物AB上,挂着35 m长的宣传条幅AE,从另一建筑物CD的顶部D处看条幅顶端A处,仰角为45°,看条幅底端E处,俯角为37°.求两建筑物间的距离BC.
(参考数据:sin37°≈0.6,cos37°≈0.8, tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
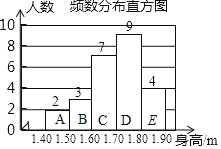
【题目】为了解学生身高,某校随机抽取了25位同学的身高,按照身高分为:A,B,C,D,E五个小组,并绘制了如下的统计图,其中每组数据均包含最小值,不包含最大值.
请结合统计图,解决下列问题:
(1)这组数据的中位数落在_____组;
(2)根据各小组的组中值,估计该校同学的平均身高;
(3)小明认为在题(2)的计算中,将D,E两组的组中值分别用1.70m和1.90m进行替换,并不影响计算结果.他的想法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】团结村在今年退耕还林活动中,计划植树160亩,全村在完成植树40亩后,某环保组织加入村民植树活动,并且该环保组织植树的速度是全村植树速度的1.5倍,整个植树过程共用了11天完成.
(1)全村每天植树多少亩?
(2)如果全村植树每天需2000元工钱,环保组织是义务植树,因此实际工钱比计划节约多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
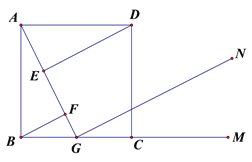
【题目】如图,正方形ABCD中,G是BC中点,DE⊥AG于E,BF⊥AG于F,GN∥DE,M是BC延长线上一点。
(1)求证:△ABF≌△DAE
(2)尺规作图:作∠DCM的平分线,交GN于点H(保留作图痕迹,不写作法和证明),试证明GH=AG。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=6,AD=8,点E是边AD上一点,EM⊥BC交AB于点M,点N在射线MB上,且AE是AM和AN的比例中项.
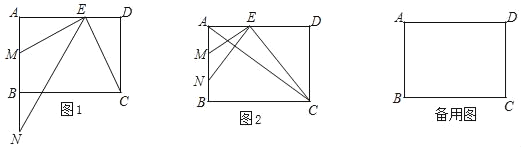
(1)如图1,求证:∠ANE=∠DCE;
(2)如图2,当点N在线段MB之间,联结AC,且AC与NE互相垂直,求MN的长;
(3)连接AC,如果△AEC与以点E、M、N为顶点所组成的三角形相似,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011山东济南,27,9分)如图,矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线![]() 经过A、C两点,与AB边交于点D.
经过A、C两点,与AB边交于点D.
(1)求抛物线的函数表达式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式,并求出m为何值时,S取得最大值;
②当S最大时,在抛物线![]() 的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com